Question

【题目】类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做等邻边四边形。．

（1）概念理解
如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是等邻边四边形。请写出你添加的一个条件；
（2）问题探究
小明猜想：对角线互相平分的等邻边四边形是菱形．她的猜想正确吗?请说明理由．
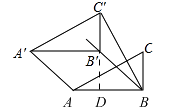
如图2，小明面了一个Rt△ABC，其中∠ABC=90°,AB=2，BC=1，井将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′．小明要是平移后的四边形ABC′A′是“等邻边四边形”应平移多少距离(即线段BB′的长)？

Answer 1

【答案】
（1）

解：答案不唯一，如：AB=BC，AB=AD，AD=CD，CD=BC；

（2）

解：小红的结论正确．

理由如下：∵四边形的对角线互相平分，

∴这个四边形是平行四边形，

∵四边形是“等邻边四边形”，

∴这个四边形有一组邻边相等，

∴这个“等邻边四边形”是菱形。

解：由∠ABC=90°，AB=2，BC=1，得：AC= ，

∵将Rt△ABC平移得到Rt△A′B′C′，

∴BB′=AA′，A′B′∥AB，A′B′=AB=2，B′C′=BC=1，A′C′=AC= ，

如下图，当AA′=AB时，BB′=AA′=AB=2；

如下图，当AA′=A′C′时，BB′=AA′=AC′= ；

如下图，当AC′=BC′= 时，延长C′B′交AB于点D，则C′B′⊥AB，

∵BB′平分∠ABC，

∴∠ABB′= ∠ABC=45°

∴∠BB′D=∠ABB′=45°，

∴B′D=BD，

设B′D=BD=x，则C′D=x+1，BB′= x

∵根据在Rt△BC′D中，BC′2=C′D2+BD2即x2+（x+1）2=5，

解得：x=1或x=-2（不合题意，舍去）；

∴BB′= x= ;

当BC′=AB=2时，与第三种情况的方法同理可得：x= 或 （不符合题意舍去）；

∴BB’= x= 。

故平移2或 或 或 。

【解析】（1）根据等邻边四边形的定义，则只需要写一对邻边相等即可；（2）根据有一组邻边相等的平行四边形是菱形去判定；根据新定义可知，有一组邻边相等即是等邻边四边形，所以要分类讨论不同相邻的边相等时的BB′的长。
【考点精析】关于本题考查的等腰三角形的性质和平行四边形的性质，需要了解等腰三角形的两个底角相等（简称：等边对等角）；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能得出正确答案．