
【题目】如图甲,在平面直角坐标系中,直线分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,⊙
,⊙![]() 的半径为
的半径为![]() 个单位长度,点
个单位长度,点![]() 为直线
为直线![]() 上的动点,过点
上的动点,过点![]() 作⊙
作⊙![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,且
,且![]() .
.
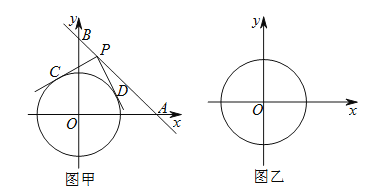
(1)判断四边形![]() 的形状并说明理由.
的形状并说明理由.
(2)求点![]() 的坐标.
的坐标.
(3)若直线![]() 沿
沿![]() 轴向左平移得到一条新的直线
轴向左平移得到一条新的直线![]() ,此直线将⊙
,此直线将⊙![]() 的圆周分得两段弧长之比为
的圆周分得两段弧长之比为![]() ,请直接写出
,请直接写出![]() 的值.
的值.
(4)若将⊙![]() 沿
沿![]() 轴向右平移(圆心
轴向右平移(圆心![]() 始终保持在
始终保持在![]() 轴上),试写出当⊙
轴上),试写出当⊙![]() 与直线
与直线![]() 有交点时圆心
有交点时圆心![]() 的横坐标
的横坐标![]() 的取值范围.(直接写出答案)
的取值范围.(直接写出答案)
【答案】(1)OCPD是正方形;(2)(2,4)或(4,2);(3)±![]() ;(4)
;(4)![]() .
.
【解析】试题分析: (1)四边形OCPD是正方形.如图,连接OC、OD.根据切线的性质和已知条件得知四边形OCPD的三个内角是90°,则该四边形是矩形.又由OC=OD,所以四边形OCPD是正方形;(2)连接OP,由![]() 为正方形,可得
为正方形,可得![]() ,设
,设![]() ,由
,由![]() 和勾股定理可得
和勾股定理可得![]() ,解得:
,解得:![]() 或
或![]() .所以
.所以![]() 点坐标为
点坐标为![]() 或
或![]() ;(3)已知平移后的新直线
;(3)已知平移后的新直线![]() 交圆于
交圆于![]() ,分得的两段弧长之比为
,分得的两段弧长之比为![]() ,可知分得的劣弧是圆周的
,可知分得的劣弧是圆周的![]() ,因直线
,因直线![]() 与
与![]() 轴夹角为
轴夹角为![]() ,
,![]() ,可得
,可得![]() ,所以当
,所以当![]() 为
为![]() 圆周时,直线与坐标轴的交点恰好是⊙
圆周时,直线与坐标轴的交点恰好是⊙![]() 与坐标轴的交点,
与坐标轴的交点,
即可得当![]() 平移到
平移到![]() 位置时,
位置时,![]() ;当
;当![]() 平移到
平移到![]() 位置时,
位置时,![]() ,所以
,所以
![]() 的值为
的值为![]() 或
或![]() ;(4)如图,⊙
;(4)如图,⊙![]() 沿
沿![]() 轴向右平移过程中分别在⊙
轴向右平移过程中分别在⊙![]() 处,⊙
处,⊙![]() 处与直线
处与直线![]() 相切,则圆在
相切,则圆在![]() 落在
落在![]() ,
,![]() 之间均满足题意,由此即可求得圆心
之间均满足题意,由此即可求得圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
试题解析:
(![]() )四边形
)四边形![]() 为正方形.
为正方形.
理由如下:连接![]() 、
、![]() ,易知
,易知![]() ,
,![]() ,
,
又![]() ,
,
∴四边形![]() 为矩形,
为矩形,
又![]() ,
,
∴四边形![]() 为正方形.
为正方形.

(![]() )连接
)连接![]() ,
,
∵![]() 为正方形,
为正方形,
∴![]() ,
,
∵![]() 在直线
在直线![]() 上,
上,
设![]() ,
,
由![]() 得:
得:
![]() ,
,
解得:![]() 或
或![]() .
.
∴![]() 点坐标为
点坐标为![]() 或
或![]() .
.
(![]() )平移后的新直线
)平移后的新直线![]() 交圆于
交圆于![]() ,分得的两段弧长之比为
,分得的两段弧长之比为![]() ,
,
∴分得的劣弧是圆周的![]() ,
,
∵直线![]() 与
与![]() 轴夹角为
轴夹角为![]() ,
,![]() ,
,
∴![]() ,
,
当![]() 为
为![]() 圆周时,直线与坐标轴的交点恰好是⊙
圆周时,直线与坐标轴的交点恰好是⊙![]() 与坐标轴的交点,
与坐标轴的交点,
当![]() 平移到
平移到![]() 位置时,
位置时,![]() ;
;
当![]() 平移到
平移到![]() 位置时,
位置时,![]() ,
,
∴![]() 的值为
的值为![]() 或
或![]() .
.
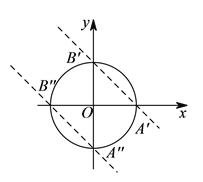
(![]() )如图,⊙
)如图,⊙![]() 沿
沿![]() 轴向右平移过程中分别在⊙
轴向右平移过程中分别在⊙![]() 处,⊙
处,⊙![]() 处与直线
处与直线![]() 相切,
相切,
则圆在![]() 落在
落在![]() ,
,![]() 之间均满足题意,
之间均满足题意,
在⊙![]() 处相切时,
处相切时,![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() .
.
∴![]() ,同理,在⊙
,同理,在⊙![]() 处相切时,
处相切时,![]() ,
,
∴![]() ,
,
∴当⊙![]() 与直线
与直线![]() 有交点时,圆心
有交点时,圆心![]() 的横坐标
的横坐标![]() 的取值范围为
的取值范围为![]() .
.
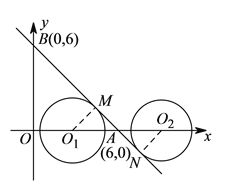


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
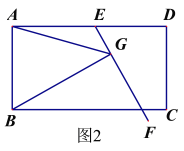
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG =AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面的材料,完成有关问题:
材料:在学习绝对值时,我们已了解绝对值的几何意义,如|5-3|表示5、3在数轴上对应的两点之间的距离;又如|5+3|=|5-(-3)|,所以|5+3|表示5、-3在数轴上对应的两点之间的距离。因此,一般地,点A,B在数轴上分别表示有理数a,b,那么A,B之间的距离(也就是线段AB的长度)可表示为|a-b|。
因此我们可以用绝对值的几何意义按如下方法求![]() 的最小值;
的最小值;
![]() 即数轴上x与1对应的点之间的距离,
即数轴上x与1对应的点之间的距离,![]() 即数轴上x与2对应的点之间的距离,把这两个距离在同一个数轴上表示出来,然后把距离相加即可得原式的值.
即数轴上x与2对应的点之间的距离,把这两个距离在同一个数轴上表示出来,然后把距离相加即可得原式的值.
设A、B、P三点对应的数分别是1、2、x.
当1≤x≤2时,即P点在线段AB上,此时![]() ;
;
当x>2时,即P点在B点右侧,此时![]() = PA+PB=AB+2PB>AB;
= PA+PB=AB+2PB>AB;
当x <1时,即P点在A点左侧,此时![]() =PA+PB=AB+2PA>AB;
=PA+PB=AB+2PA>AB;
综上可知,当1≤x≤2时(P点在线段AB上),![]() 取得最小值为1.
取得最小值为1.
![]()
![]()
![]()
请你用上面的思考方法结合数轴完成以下问题:
(1)满足![]() 的x的取值范围是 。
的x的取值范围是 。
(2)求![]() 的最小值为 ,最大值为 。
的最小值为 ,最大值为 。
备用图:
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应学校提出的“节能减排,低碳生活”的倡议,班会课上小李建议每位同学都践行“双面打印,节约用纸”.他举了一个实际例子:打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,总质量为160克.已知每页薄型纸比厚型纸轻0.8克,求例子中的A4厚型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .
.

(1)先作![]() 的平分线交
的平分线交![]() 边于点
边于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 长为半径作⊙
长为半径作⊙![]() .
.
(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中![]() 与⊙
与⊙![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(3)若![]() ,
,![]() ,求出(1)中⊙
,求出(1)中⊙![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,点D、E分别是边AB、AC的中点,将△ADE绕点A旋转,BD与CE所在的直线交于点F.
(1)如图(2)所示,将△ADE绕点A逆时针旋转,且旋转角不大于60°,∠CFB的度数是多少?说明你的理由?
(2)当△ADE绕点A旋转时,若△BCF为直角三角形,求出线段BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com