
【题目】如图,在![]() 中,
中,![]() .
.

(1)先作![]() 的平分线交
的平分线交![]() 边于点
边于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 长为半径作⊙
长为半径作⊙![]() .
.
(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中![]() 与⊙
与⊙![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(3)若![]() ,
,![]() ,求出(1)中⊙
,求出(1)中⊙![]() 的半径.
的半径.
科目:初中数学 来源: 题型:
【题目】某学校准备购买A、B两种型号篮球,询问了甲、乙两间学校了解这两款篮球的价格,下表是甲、乙两间学校购买A、B两种型号篮球的情况:
购买学校 | 购买型号及数量(个) | 购买支出款项(元) | |
A | B | ||
甲 | 3 | 8 | 622 |
乙 | 5 | 4 | 402 |
(1)求A、B两种型号的篮球的销售单价;
(2)若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个,求A种型号的篮球最少能采购多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b在数轴上的位置如图所示,且|a|<|b|,下列各式中正确的个数是( )
①a+b<0;②b﹣a>0;③![]() ;④3a﹣b>0;⑤﹣a﹣b>0.
;④3a﹣b>0;⑤﹣a﹣b>0.
![]()
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习绝对值后,我们知道,![]() 表示数
表示数![]() 在数轴上的对应点与原点的距离. 如:
在数轴上的对应点与原点的距离. 如:![]() 表示5在数轴上的对应点到原点的距离.而
表示5在数轴上的对应点到原点的距离.而![]() ,即
,即![]() 表示5、0在数轴上对应的两点之间的距离.类似的,有:
表示5、0在数轴上对应的两点之间的距离.类似的,有:![]() 表示5、3在数轴上对应的两点之间的距离;
表示5、3在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示5、
表示5、![]() 在数轴上对应的两点之间的距离. 一般地,点A、B在数轴上分别表示有理数
在数轴上对应的两点之间的距离. 一般地,点A、B在数轴上分别表示有理数![]() 、
、![]() ,那么A、B之间的距离可表示为
,那么A、B之间的距离可表示为![]() .
.
请根据绝对值的意义并结合数轴解答下列问题:
(1)数轴上表示2和5的两点之间的距离是______;数轴上表示1和-3的两点之间的距离是 ;
(2)数轴上P、Q两点的距离为3,且点P表示的数是2,则点Q表示的数是___________.
(3)点A、B、C在数轴上分别表示有理数![]() 、
、![]() 、1,那么A到B的距离与A到C的距离之和可表示为 ;
、1,那么A到B的距离与A到C的距离之和可表示为 ;
(4)满足![]() 的整数
的整数![]() 的值为 .
的值为 .
(5)![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在平面直角坐标系中,直线分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,⊙
,⊙![]() 的半径为
的半径为![]() 个单位长度,点
个单位长度,点![]() 为直线
为直线![]() 上的动点,过点
上的动点,过点![]() 作⊙
作⊙![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,且
,且![]() .
.
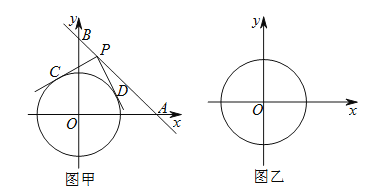
(1)判断四边形![]() 的形状并说明理由.
的形状并说明理由.
(2)求点![]() 的坐标.
的坐标.
(3)若直线![]() 沿
沿![]() 轴向左平移得到一条新的直线
轴向左平移得到一条新的直线![]() ,此直线将⊙
,此直线将⊙![]() 的圆周分得两段弧长之比为
的圆周分得两段弧长之比为![]() ,请直接写出
,请直接写出![]() 的值.
的值.
(4)若将⊙![]() 沿
沿![]() 轴向右平移(圆心
轴向右平移(圆心![]() 始终保持在
始终保持在![]() 轴上),试写出当⊙
轴上),试写出当⊙![]() 与直线
与直线![]() 有交点时圆心
有交点时圆心![]() 的横坐标
的横坐标![]() 的取值范围.(直接写出答案)
的取值范围.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, ![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标为
的坐标为![]() .
.

(1)把![]() 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的![]() ,画出
,画出![]() ,并写出
,并写出![]() 的坐标;
的坐标;
(2)以原点![]() 为对称中心,再画出与
为对称中心,再画出与![]() 关于原点
关于原点![]() 对称的
对称的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com