
ЁОЬтФПЁПдкОрРыДѓзуГЧЧјЕФ1.5ЙЋРяЕФББЩНжЎЩЯЃЌгавЛДІУмШчЗхЗПЕФЪЏПпдьЯёЕуЃЌНёБЛГЦЮЊББЩНЪЏПпЃЎББЩНЪЏПпдьЯёдкСНЫЮЪБЦкДяЕНЖІЪЂЃЌж№НЅЖМГЩСЫвдББЩНЗ№ЭхЮЊжааФЃЌЛЗШЦгЊХЬЦТЁЂЗ№ЖњбвЃЌЙлвєЦТЁЂЖрБІЫўЕШЖрДІдьЯёЕуЕФДѓаЭЪЏПпШКЃЎЖрБІЫўЃЌвВГЦЮЊЁААзЫўЁБЁАББЫўЁБЃЌгкбвЪЏжЎЩЯЃЌЮЊАЫНЧаЮИѓЪНзЉЫўЃЌЭтЙлПЩБцЪЎЖўМЖЃЌЦфФкгаАЫВуТЅИѓЃЌПЩбизХЫўаФФкЕФЬнЕРж№МЖЖјЩЯЃЌдЊЧвЦкМфЃЌаЁЛЊКЭТшТшЕНДѓзуББЩНгЮЭцЃЌаЁЛЊеОдкЦТЖШЮЊlЃН1ЃК2ЕФЩНЦТЩЯЕФBЕуЙлПДЗчОАЃЌЧЁКУПДЕНЖдУцЕФЖрБІХрЃЌВтЕУблОІAПДЕНЫўЖЅCЕФбіНЧЮЊ30ЁуЃЌНгзХаЁЛЊгжЯђЯТзпСЫ10![]() УзЃЌИеКУЕНДяЦТЕзEЃЌетЪБПДЕНЫўЖЅCЕФбіНЧЮЊ45ЁуЃЌШєABЃН1.5УзЃЌдђЖрБІЫўЕФИпЖШCDдМЮЊЃЈЁЁЁЁЃЉЃЈОЋШЗЕН0.1УзЃЌВЮПМЪ§Он
УзЃЌИеКУЕНДяЦТЕзEЃЌетЪБПДЕНЫўЖЅCЕФбіНЧЮЊ45ЁуЃЌШєABЃН1.5УзЃЌдђЖрБІЫўЕФИпЖШCDдМЮЊЃЈЁЁЁЁЃЉЃЈОЋШЗЕН0.1УзЃЌВЮПМЪ§Он![]() Ёж1.732ЃЉ
Ёж1.732ЃЉ

A. 51.0УзB. 52.5УзC. 27.3УзD. 28.8Уз
ЁОД№АИЁПB
ЁОНтЮіЁП
ШчЭМЃЌЩшCDЃНxУзЃЎбгГЄABНЛDEгкHЃЌзїAMЁЭCDгкMЃЌAЁфNЁЭCDгкNЃЎЯыАьЗЈЙЙНЈЗНГЬЧѓГіxМДПЩЃЎ
НтЃКШчЭМЃЌЩшCDЃНxУзЃЎбгГЄABНЛDEгкHЃЌзїAMЁЭCDгкMЃЌAЁфNЁЭCDгкNЃЎ
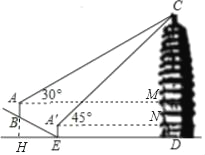
дкRtЁїBHEжаЃЌЁпBEЃН10![]() УзЃЌBHЃКEHЃН1ЃК2ЃЌ
УзЃЌBHЃКEHЃН1ЃК2ЃЌ
ЁрBHЃН10ЃЈУзЃЉЃЌEHЃН20ЃЈУзЃЉЃЌ
ЁпЫФБпаЮAHDMЪЧОиаЮЃЌЫФБпаЮAЁфEDNЪЧОиаЮЃЌ
ЁрAMЃНDHЃЌAHЃНDMЃЌAЁфNЃНDEЃЌAЁфEЃНDNЃН1.5ЃЈУзЃЉЃЌ
дкRtЁїCAЁфNжаЃЌЁпЁЯCAЁфNЃН45ЁуЃЌ
ЁрCNЃНAЁфNЃНDEЃНЃЈxЉ1.5ЃЉЃЈУзЃЉЃЌ
ЁпAMЃНDHЃНЃЈ20+xЉ1.5ЃЉЃЈУзЃЉЃЌCMЃНЃЈxЉ5ЃЉЃЈУзЃЉЃЌ
дкRtЁїACMжаЃЌЁпЁЯCAMЃН30ЁуЃЌ
ЁрAMЃН![]() CMЃЌ
CMЃЌ
Ёр20+xЉ1.5ЃН![]() ЃЈxЉ11.5ЃЉЃЌ
ЃЈxЉ11.5ЃЉЃЌ
ЁрxЁж52.5ЃЌ
ЙЪбЁЃКBЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛЦНУцжБНЧзјБъЯЕжаЃЌКЏЪ§yЃНax2+bxгыyЃНbx+aЕФЭМЯѓПЩФмЪЧЃЈЁЁЁЁЃЉ
A. 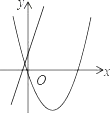 B.
B. 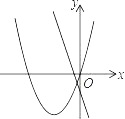 C.
C. 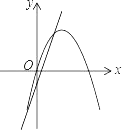 D.
D. 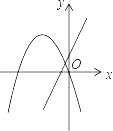
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
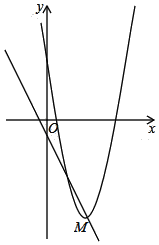
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊЕуMЃЌNЕФзјБъЗжБ№ЮЊЃЈЉ1ЃЌ2ЃЉЃЌЃЈ2ЃЌ1ЃЉЃЌШєХзЮяЯпy=ax2Љx+2ЃЈaЁй0ЃЉгыЯпЖЮMNгаСНИіВЛЭЌЕФНЛЕуЃЌдђaЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A. aЁмЉ1Лђ![]() ЁмaЃМ
ЁмaЃМ![]() B.
B. ![]() ЁмaЃМ
ЁмaЃМ![]()
C. aЁм![]() ЛђaЃО
ЛђaЃО![]() D. aЁмЉ1ЛђaЁн
D. aЁмЉ1ЛђaЁн![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ЕФЖЅЕуMдкжБЯпLЃК
ЕФЖЅЕуMдкжБЯпLЃК![]() ЩЯЃЎ
ЩЯЃЎ
![]() ЧѓжБЯпLЕФКЏЪ§БэДяЪНЃЛ
ЧѓжБЯпLЕФКЏЪ§БэДяЪНЃЛ
![]() ЯжНЋХзЮяЯпбиИУжБЯпLЗНЯђНјааЦНвЦЃЌЦНвЦКѓЕФХзЮяЯпЕФЖЅЕуЮЊNЃЌгыxжсЕФгвНЛЕуЮЊCЃЌСЌНгNCЃЌЕБ
ЯжНЋХзЮяЯпбиИУжБЯпLЗНЯђНјааЦНвЦЃЌЦНвЦКѓЕФХзЮяЯпЕФЖЅЕуЮЊNЃЌгыxжсЕФгвНЛЕуЮЊCЃЌСЌНгNCЃЌЕБ![]() ЪБЃЌЧѓЦНвЦКѓЕФХзЮяЯпЕФНтЮіЪНЃЎ
ЪБЃЌЧѓЦНвЦКѓЕФХзЮяЯпЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABгыЁбOЯрЧагкЕуCЃЌOAЃЌOBЗжБ№НЛЁбOгкЕуD,EЃЌЛЁCD=ЛЁCEЃЎ
ЃЈ1ЃЉЧѓжЄЃКOA=OB
ЃЈ2ЃЉвбжЊAB=4![]() ЃЌOA=4ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЎ
ЃЌOA=4ЃЌЧѓвѕгАВПЗжЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгЩгкЪРНчШЫПкдіГЄЁЂЫЎЮлШОвдМАЫЎзЪдДРЫЗбЕШдвђЃЌШЋЪРНчУцСйзХЕЫЎзЪдДВЛзуЕФЮЪЬтЃЌЮвЙњЪЧЪРНчЩЯбЯжиШБЫЎЕФЙњМвжЎвЛЃЌШЫОљеМЫЎСПНіЮЊ2400m3зѓгвЃЌЮвЙњвбБЛСЊКЯЙњСаЮЊ13ИіЦЖЫЎЙњМвжЎвЛЃЌКЯРэРћгУЫЎзЪдДЪЧШЫРрПЩГжајЗЂеЙЕФЕБЮёжЎМБЃЌЖјНкдМгУЫЎЪЧЫЎзЪдДКЯРэРћгУЕФЙиМќЫљдкЃЌЪЧзюПьНнЁЂзюгааЇЁЂзюПЩааЕФЮЌЛЄЫЎзЪдДПЩГжајРћгУЕФЭООЖжЎвЛЃЌЮЊСЫЕїВщОгУёЕФгУЫЎЧщПіЃЌгаЙиВПУХЖдФГаЁЧјЕФ20ЛЇОгУёЕФдТгУЫЎСПНјааСЫЕїВщЃЌЪ§ОнШчЯТЃКЃЈЕЅЮЛЃКtЃЉ
6.7 | 8.7 | 7.3 | 11.4 | 7.0 | 6.9 | 11.7 | 9.7 | 10.0 | 9.7 |
7.3 | 8.4 | 10.6 | 8.7 | 7.2 | 8.7 | 10.5 | 9.3 | 8.4 | 8.7 |
ећРэЪ§Он АДШчЯТЗжЖЮећРэбљБОЪ§ОнВЂВЙжСБэИёЃКЃЈБэ1ЃЉ
гУЫЎСПxЃЈtЃЉ | 6.0ЁмxЃМ7.5 | 7.5ЁмxЃМ9.0 | 9.0ЁмxЃМ10.5 | 10.5ЁмxЃМ12 |
ШЫЪ§ | a | 6 | b | 4 |
ЗжЮіЪ§ОнЃЌВЙШЋЯТСаБэИёжаЕФЭГМЦСПЃЛЃЈБэ2ЃЉ
ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ |
8.85 | c | d |
ЕУГіНсТлЃК
ЃЈ1ЃЉБэжаЕФaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЌcЃНЁЁ ЁЁЃЌdЃНЁЁ ЁЁЃЎ
ЃЈ2ЃЉШєгУБэ1жаЕФЪ§ОнжЦзївЛИіЩШаЮЭГМЦЭМЃЌдђ9.0ЁмxЃМ10.5ЫљЪОЕФЩШаЮдВаФНЧЕФЖШЪ§ЮЊЁЁ ЁЁЖШЃЎ
ЃЈ3ЃЉШчЙћИУаЁЧјгазЁЛЇ400ЛЇЃЌЧыИљОнбљБОЙРМЦгУЫЎСПдк6.0ЁмxЃМ9.0ЕФОгУёгаЖрЩйЛЇЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНУћЭЌбЇдквЛДЮгУЦЕТЪШЅЙРМЦИХТЪЕФЪЕбщжаЃЌЛцГіСЫФГвЛНсЙћГіЯжЕФЦЕТЪЕФелЯпЭМЃЌдђЗћКЯетвЛНсЙћЕФЪЕбщПЩФмЪЧ
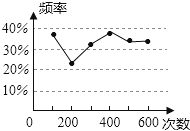
A. жРвЛУЖе§СљУцЬхЕФїЛзгЃЌГіЯж1ЕуЕФИХТЪ
B. ХзвЛУЖгВБвЃЌГіЯже§УцЕФИХТЪ
C. ШЮвтаДвЛИіећЪ§ЃЌЫќФмБЛ2ећГ§ЕФИХТЪ
D. ДгвЛИізАга2ИіАзЧђКЭ1ИіКьЧђЕФДќзгжаШЮШЁвЛЧђЃЌШЁЕНКьЧђЕФИХТЪ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
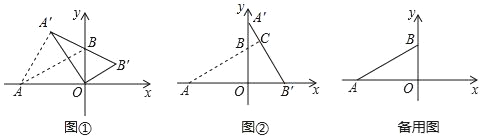
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊдЕуЃЌЕуAЃЈЉ![]() ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌ1ЃЉАбЁїABOШЦЕуOЫГЪБеыа§зЊЃЌЕУЁїA'B'OЃЌЕуAЃЌBа§зЊКѓЕФЖдгІЕуЮЊA'ЃЌB'ЃЌМЧа§зЊНЧЮЊІСЃЈ0ЁуЃМІСЃМ360ЁуЃЉЃЎ
ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌ1ЃЉАбЁїABOШЦЕуOЫГЪБеыа§зЊЃЌЕУЁїA'B'OЃЌЕуAЃЌBа§зЊКѓЕФЖдгІЕуЮЊA'ЃЌB'ЃЌМЧа§зЊНЧЮЊІСЃЈ0ЁуЃМІСЃМ360ЁуЃЉЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕБЕуAЁфЃЌBЃЌBЁфЙВЯпЪБЃЌЧѓAAЁфЕФГЄЃЎ
ЃЈ2ЃЉШчЭМЂкЃЌЕБІСЃН90ЁуЃЌЧѓжБЯпABгыAЁфBЁфЕФНЛЕуCЕФзјБъЃЛ
ЃЈ3ЃЉЕБЕуAЁфдкжБЯпABЩЯЪБЃЌЧѓBBЁфгыOAЁфЕФНЛЕуDЕФзјБъЃЈжБНгаДГіНсЙћМДПЩЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() Й§Еу
Й§Еу![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊ
ЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊ![]() ЃЌзї
ЃЌзї![]() жсгкЕу
жсгкЕу![]() .ЩшЕу
.ЩшЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЈВЛгыЕу
ЩЯЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЈВЛгыЕу![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() зї
зї![]() жсЕФЦНааЯпЃЌНЛжБЯп
жсЕФЦНааЯпЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌзї
ЃЌзї![]() гкЕу
гкЕу![]() .
.

ЃЈ1ЃЉЬюПеЃК![]() __________ЃЌ
__________ЃЌ![]() __________ЃЌ
__________ЃЌ![]() __________ЃЛ
__________ЃЛ
ЃЈ2ЃЉЬНОПЃКЪЧЗёДцдкетбљЕФЕу![]() ЃЌЪЙЫФБпаЮ
ЃЌЪЙЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіЕу
ЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩш![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГі
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГі![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com