
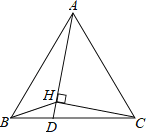
【题目】如图,△ABC是等边三角形,AB=![]() ,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
,点D是边BC上一点,点H是线段AD上一点,连接BH、CH.当∠BHD=60°,∠AHC=90°时,DH=_____.
【答案】![]()
【解析】如图,作AE⊥BH于E,BF⊥AH于F,利用等边三角形的性质得AB=AC,∠BAC=60°,再证明∠ABH=∠CAH,则可根据“AAS”证明△ABE≌△CAH,所以BE=AH,AE=CH,在Rt△AHE中利用含30度的直角三角形三边的关系得到HE=![]() AH,AE=
AH,AE=![]() AH,则CH=
AH,则CH=![]() AH,于是在Rt△AHC中利用勾股定理可计算出AH=2,从而得到BE=2,HE=1,AE=CH=
AH,于是在Rt△AHC中利用勾股定理可计算出AH=2,从而得到BE=2,HE=1,AE=CH=![]() ,BH=1,接下来在Rt△BFH中计算出HF=
,BH=1,接下来在Rt△BFH中计算出HF=![]() ,BF=
,BF=![]() ,然后证明△CHD∽△BFD,利用相似比得到
,然后证明△CHD∽△BFD,利用相似比得到![]() =2,从而利用比例性质可得到DH的长.
=2,从而利用比例性质可得到DH的长.
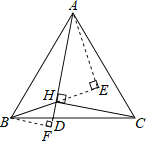
作AE⊥BH于E,BF⊥AH于F,如图,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵∠BHD=∠ABH+∠BAH=60°,∠BAH+∠CAH=60°,
∴∠ABH=∠CAH,
在△ABE和△CAH中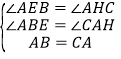 ,
,
∴△ABE≌△CAH,
∴BE=AH,AE=CH,
在Rt△AHE中,∠AHE=∠BHD=60°,
∴sin∠AHE=![]() ,HE=
,HE=![]() AH,
AH,
∴AE=AHsin60°=![]() AH,
AH,
∴CH=![]() AH,
AH,
在Rt△AHC中,AH2+(![]() AH)2=AC2=(
AH)2=AC2=(![]() )2,解得AH=2,
)2,解得AH=2,
∴BE=2,HE=1,AE=CH=![]() ,
,
∴BH=BE﹣HE=2﹣1=1,
在Rt△BFH中,HF=![]() BH=
BH=![]() ,BF=
,BF=![]() ,
,
∵BF∥CH,
∴△CHD∽△BFD,
∴![]() =2,
=2,
∴DH=![]() HF=
HF=![]() ×
×![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
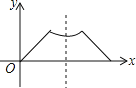
【题目】已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
A. 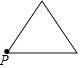 B.
B.  C.
C. 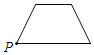 D.
D. 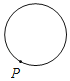
查看答案和解析>>
科目:初中数学 来源: 题型:
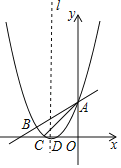
【题目】如图,抛物线y=![]() x2+bx+c与直线y=
x2+bx+c与直线y=![]() x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求
(1)∠BAE的度数.
(2)∠DAE的度数.
(3)探究:有的同学认为无论∠B、∠C的度数是多少,都有∠DAE=![]()
![]() (∠B-∠C)成立,你同意吗?并说出成立或不成立的理由.
(∠B-∠C)成立,你同意吗?并说出成立或不成立的理由.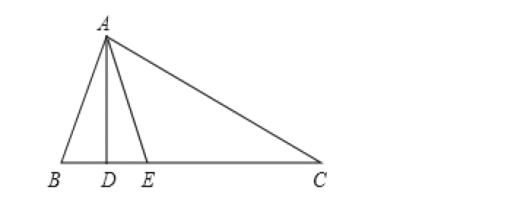
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
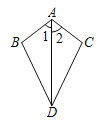
A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
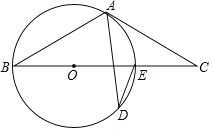
【题目】如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点.
(1)若∠ADE=25°,求∠C的度数;
(2)若AB=AC,CE=2,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+(a﹣2)x+3的图象与一次函数y=x(1≤x≤2)的图象有且仅有一个交点,则实数a的取值范围是( )
A. a=3±2![]() B. ﹣1≤a<2
B. ﹣1≤a<2
C. a=3![]() 或﹣
或﹣![]() ≤a<2 D. a=3﹣2
≤a<2 D. a=3﹣2![]() 或﹣1≤a<﹣
或﹣1≤a<﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒4°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒6°的速度旋转,直线MN保持不动,如图2,设旋转时间为t(0≤t≤60,单位:秒).
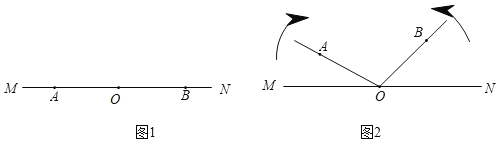
(1)当t=3时,求∠AOB的度数;
(2)在运动过程中,当∠AOB第二次达到72°时,求t的值;
(3)在旋转过程中是否存在这样的t,使得射线OB与射线OA垂直?如果存在,请求出t的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com