Question

7．如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从A开始沿折线AC→CB→BA运动，点P在AC，CB，BA边上运动的速度分别为每秒3，4，5个单位．直线l从与AC重合的位置开始，以每秒$\frac{4}{3}$个单位的速度沿CB方向平行移动，即移动过程中保持l∥AC，且分别与CB，AB边交于E，F两点，点P与直线l同时出发，设运动的时间为t秒，当点P第一次回到点A时，点P与直线l同时停止运动．当点P在BA边上运动时，作点P关于直线EF的对称点，记为点Q，若形成的四边形PEQF为菱形，则t=$\frac{6}{5}$或$\frac{30}{7}$．

Answer 1

分析 首先结合题意画出图形，然后根据菱形的性质和相似三角形的性质分别从两种情况当P点在AC上时和当P在AB上时去分析求解，即可求得t的值．

解答 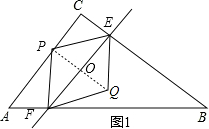解：如图1，当P点在AC上时，（0＜t≤2）
∴AP=3t，PC=6-3t，EC=$\frac{4}{3}$t，
∴BE=8-$\frac{4}{3}$t，
∵EF∥AC，
∴△FEB∽△ACB，
∴$\frac{EF}{AC}=\frac{BE}{BC}$，
∴$\frac{EF}{6}=\frac{8-\frac{4}{3}t}{8}$，
∴EF=6-t．
∵四边形PEQF是菱形，
∴∠POE=90°，OE=$\frac{1}{2}$EF=3-$\frac{1}{2}$t，
∵EF∥AC，∠C=90°，
∴∠OEC=90°，
∴四边形PCEO是矩形，
∴OE=PC．
∴3-$\frac{1}{2}$t=6-3t，
∴t=$\frac{6}{5}$，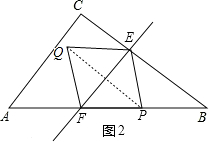
如图2，当P在AB上时（4＜t＜6），
∵四边形PFQE是菱形，
∴PE=PF，
∴∠PFE=∠PEF，
∵EF∥AC，∠C=90°，
∴∠FEB=∠FEP+∠PEB=90°，
∴∠B+∠EFB=90°，
∴∠B+∠FEP=90°，
∴∠PEB=∠B，
∴PE=PB．
∵PB=5（t-4），
∴BF=10（t-4），
∵sin∠B=$\frac{3}{5}$=$\frac{EF}{BF}$，
∴$\frac{EF}{10（t-4）}=\frac{3}{5}$，
∴EF=6t-24
∵CE=$\frac{4}{3}$t，
∴BE=8-$\frac{4}{3}$t，
∵△FEB∽△ACB，
∴$\frac{EF}{AC}=\frac{BE}{BC}$，
∴$\frac{EF}{6}=\frac{8-\frac{4}{3}t}{8}$，
∴EF=6-t．
∴6-t=6t-24
解得t=$\frac{30}{7}$；
∴t的值为$\frac{6}{5}$或$\frac{30}{7}$．
故答案为：$\frac{6}{5}$或$\frac{30}{7}$．

点评 此题属于相似三角形的综合题，考查了相似三角形的判定与性质，菱形的性质、矩形的判定与性质以及三角函数等知识．注意结合题意画出图形，利用图形求解是关键．