
����Ŀ��ij����Ϊ��ǿѧ�����ʣ���չ��������������������չ�Կγ��Թ�ѧ��ѡ��ÿλѧ��������������ѡ��һ����б�����ѡ�ν��������꼶ѧ��ѡ�ν�����Ƴ���������ʾ������ͳ��ͼ��������Ϣδ����������֪��У���꼶����������Ů����15�ˣ�Ů��ѡ����������������ѡ������������3����

��1�����У���꼶Ů��������
��2����ȫ����ͳ��ͼ��
��3��С�����㣬���ְ��꼶ѧ��ѡ�����������ռ���꼶ѧ��������������֮һ��С����ΪȫУ������֮һ��ѧ��ѡ������������ΪС���뷨������Ϊʲô��
���𰸡���1����У���꼶Ů������Ϊ75�ˣ���2������������3����������������
��������
��1���ȸ������������ѡ�������Ů��������������ѡ�������Ů������������ռ�İٷֱȼ��ɵõ����꼶Ů����������
��2����Ů��������15�õ����꼶����������������������������ȥѡ�����������������ɵõ�ѡ������������ٲ�ȫ����ͳ��ͼ���ɣ�
��3����������ֻѡ���˰��꼶�������д����Լ��ɵõ����ۣ�
�⣺��1����Ů��ѡ����������������ѡ������������3��,
���������ͼ�õ�Ů��ѡ�����������Ϊ����15��3���ˣ�
��Ů��ѡ�����������������ռ�İٷֱȵõ����꼶Ů��������Ϊ��
��15��3����60%��75���ˣ���
�𣺸�У���꼶Ů������Ϊ75�ˣ�
��2���������⣬���(1)�Ľ���õ���
���꼶����ѡ����������Ϊ75+15��40��15��35���ˣ���
��ȫ����ͳ��ͼ��ͼ��ʾ��
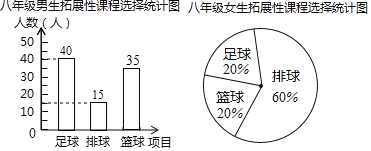
��3����������
��Ϊ����ֻѡ���˰��꼶�������д����ԣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ֱ֪��������ABC�Ķ���A������Ϊ��-2��1��������B������Ϊ��-5��4��������ABC����ƽ��5����λ��������ƽ��3����λ��õ�![]() ��
��
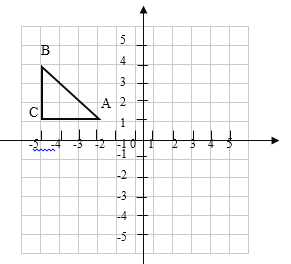
��1����ֱ��д����C�����ꣻ
��2���뻭��![]() ��
��
��3������P��x���ϣ���![]() ���ABC�������ȣ�ֱ��д����P�����꣮
���ABC�������ȣ�ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BC��5��E��F�ֱ���AB��AC���е㣬����P������EF�ϣ�BP��CE�ڵ�D����CBP��ƽ���߽�CE�ڵ�Q����CQ��![]() CEʱ��EP+BP��ֵΪ��������
CEʱ��EP+BP��ֵΪ��������
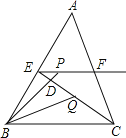
A.10B.8C.6D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У����κ���y����![]() x2+bx+c��ͼ����A��4��0����C��0��2����
x2+bx+c��ͼ����A��4��0����C��0��2����
��1���������ߵı���ʽ��
��2����ͼ1����E�ǵ�һ�����������ϵ�һ�����㣮����ACE������ʱ���������E�����ꣻ
��3����ͼ2�������������Ƿ����һ��P��ʹ��CAP��45���������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
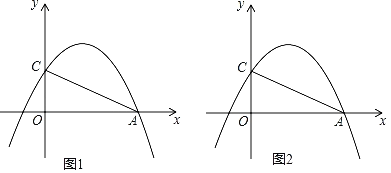
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD���ָ������С���٢ڣ���һ��С�����ۣ�ȥ���ۺٺ͢ڿɼ�ƴ��һ���µ����Σ���EF��AD��2��BC��EF��1����AB�ij��ǣ� ��
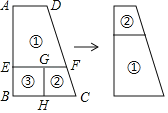
A.6B.3![]() C.9D.3
C.9D.3![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���G�ǵȱ�������AOB�����ģ���A�ڵ�һ���ޣ���B����Ϊ(4��0)������OG��������y��ax��x��2��+1+![]() �Ķ���ΪP��
�Ķ���ΪP��
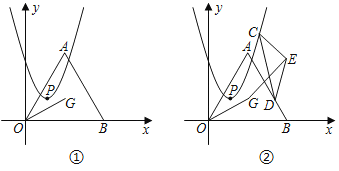
��1��ֱ��д����A�������������ߵĶԳ��
��2������OP����AOG��2��AOPʱa��ֵ��
��3����ͼ�ڣ��������߿������ϣ���C��D�ֱ�Ϊ�����ߺ��߶�AB�ϵĶ��㣬��CDΪ�ױ߹��춥��Ϊ120���ĵ���������CDE����C��D��E����ʱ��˳������GE��
�ٵ�Q��x���ϣ����ı���GDQOΪƽ���ı���ʱ����GQ��ֵ��
�ڵ�GE����СֵΪ1ʱ���������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���A��90�㣬��D��E�ֱ���AC��BC�ϣ���CD��BC��AC��CE����EΪԲ�ģ�DE��Ϊ�뾶��Բ����E������B����AB��BC�ֱ��ڵ�F��G��
��1����֤��AC�ǡ�E�����ߣ�
��2����AF��4��CG��5��
�����E�İ뾶��
����Rt��ABC������ԲԲ��ΪI����IE�� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ���E��F�ֱ���AB��BC�ϣ���ED//BC��EF//AC��
(1)��֤��BE=DE��
(2)��AB=ACʱ����˵���ı���EFCDΪ���Σ�
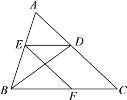
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������һ������ʵ�飺��һ�����������������4����ͬ��С�����Ϸֱ��������0��10��20��30��Ȼ����������Ⱥ���������С��һ�������Żأ���
��1������������С�������������֮������Ϊ �����Ϊ ��
��2�������û���״ͼ���б��ķ������������������С�������������֮�Ͳ�����30�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com