
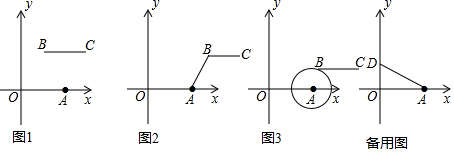
分析 (1)理解新定义,按照新定义的要求求出两个距离值;
(2)如答图2所示,当点B落在⊙A上时,m的取值范围为2≤m≤6:
当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2;
当2≤m<4时,作BN⊥x轴于点N,线段BC与线段OA的距离等于BN长;
(3)①在准确理解点M运动轨迹的基础上,画出草图,如答图3所示.由图形可以直观求出封闭图形的周长;
②如答图4所示,符合题意的相似三角形有三个,需要进行分类讨论,分别利用点的坐标关系以及相似三角形比例线段关系求出m的值.
解答 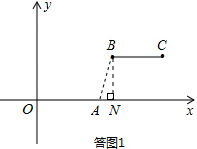 解:(1)当m=2,n=2时,
解:(1)当m=2,n=2时,
如题图1,线段BC与线段OA的距离(即线段BN的长)=2;
当m=5,n=2时,
B点坐标为(5,2),线段BC与线段OA的距离,即为线段AB的长,
如答图1,过点B作BN⊥x轴于点N,则AN=1,BN=2,
在Rt△ABN中,由勾股定理得:AB=$\sqrt{A{N}^{2}+B{N}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$;
故答案为:2,$\sqrt{5}$;
(2)如答图2所示,当点B落在⊙A上时,m的取值范围为2≤m≤6: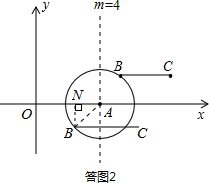
当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2;
当2≤m<4时,作BN⊥x轴于点N,线段BC与线段OA的距离等于BN长,
ON=m,AN=OA-ON=4-m,在Rt△ABN中,由勾股定理得:
∴d=$\sqrt{{2}^{2}-(4-m)^{2}}$=$\sqrt{4-16+8m-{m}^{2}}$=$\sqrt{-{m}^{2}+8m-12}$.
(3)存在.
∵m≥0,n≥0,∴点M位于第一象限.
∵A(4,0),D(0,2),∴OA=2OD.
如答图4所示,相似三角形有三种情形: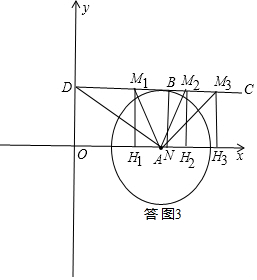
(I)△AM1H1,此时点M纵坐标为2,点H在A点左侧.
如图,OH1=m+2,M1H1=2,AH1=OA-OH1=2-m,
由相似关系可知,M1H1=2AH1,即2=2(2-m),
∴m=1;
(II)△AM2H2,此时点M纵坐标为2,点H在A点右侧.
如图,OH2=m+2,M2H2=2,AH2=OH2-OA=m-2,
由相似关系可知,M2H2=2AH2,即2=2(m-2),
∴m=3;
(III)△AM3H3,此时点B落在⊙A上.
如图,OH3=m+2,AH3=OH3-OA=m-2,
过点B作BN⊥x轴于点N,则BN=M3H3=n,AN=m-4,
由相似关系可知,AH3=2M3H3,即m-2=2n (1)
在Rt△ABN中,由勾股定理得:22=(m-4)2+n2 (2)
由(1)、(2)式解得:m1=$\frac{26}{5}$,m2=2,
当m=2时,点M与点A横坐标相同,点H与点A重合,故舍去,
∴m=$\frac{26}{5}$.
综上所述,存在m的值使以A、M、H为顶点的三角形与△AOD相似,m的取值为:1或3或$\frac{26}{5}$.
点评 本题考查了圆的相关性质、点的坐标、勾股定理等重要知识点,根据新定义得出线段之间距离是解决本题的关键.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
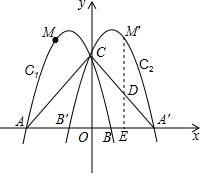 如图,抛物线C1:y=ax2+bx+4与x轴交于A(-3,0),B两点,与y轴交于点C,点M(-$\frac{3}{2}$,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.
如图,抛物线C1:y=ax2+bx+4与x轴交于A(-3,0),B两点,与y轴交于点C,点M(-$\frac{3}{2}$,5)是抛物线C1上一点,抛物线C2与抛物线C1关于y轴对称,点A、B、M关于y轴的对称点分别为点A′、B′、M′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
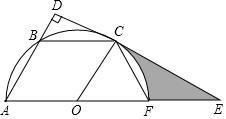 如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
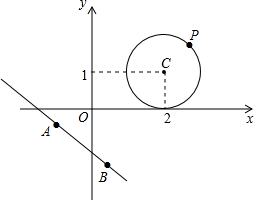 阅读材料:
阅读材料:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20 | B. | 24 | C. | 28 | D. | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com