
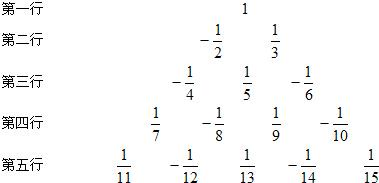
���� �������֪���ڼ��о��м��������ҷ�ĸ��ż�������Ǹ�����
��1����8�еĵ�һ�����ķ�ĸ��1+2+3+��+7+1=29�����8�еĵ�4�����ķ�ĸ��32��
��2��12�еĵ�һ�����ķ�ĸ��1+2+3+��+11+1=67�����11�����ķ�ĸ��67+10=77����ڸ�����$\frac{1}{77}$��
��� �⣺��1����1+2+3+��+7+1=$\frac{7��8}{2}$+1=29��32-29+1=4��
��-$\frac{1}{32}$�ǵ�8�����������ҵ�4������
��2��1+2+3+��+11+1=$\frac{11��12}{2}$+1=67�����11�����ķ�ĸ��67+10=77����11������$\frac{1}{77}$��
�ʴ�Ϊ��8��4��$\frac{1}{77}$��
���� ���⿼�������ֵı仯���ɣ�ע��ֱ������ľ���ֵ���ɺ����ķ��ű仯���ɣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
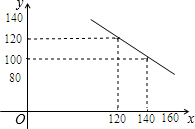 ij�̵�����һ�ֳɱ�����Ϊ100Ԫ/�����˶������涨����ʱ�����۵��۲����ڳɱ����ۣ��ֲ�����180Ԫ/�������г����飬����������y�����������۵���x��Ԫ��֮��Ĺ�ϵ����һ�κ���y=kx+b��k��0������ͼ����ͼ��
ij�̵�����һ�ֳɱ�����Ϊ100Ԫ/�����˶������涨����ʱ�����۵��۲����ڳɱ����ۣ��ֲ�����180Ԫ/�������г����飬����������y�����������۵���x��Ԫ��֮��Ĺ�ϵ����һ�κ���y=kx+b��k��0������ͼ����ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x3��23 | B�� | -xy2��$\frac{1}{4}$yx2 | C�� | 7��-$\frac{1}{3}$ | D�� | ab��7a |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com