
【题目】如图,已知△ACE是等腰直角三角形,∠ACE=90°,B点为AE上一点,△CAB经过逆时针旋转后到达△CED的位置.
问:(1)旋转中心是哪个点?旋转角是哪个角?旋转了多少度?
(2)图中哪两个三角形全等?
(3)若∠ACB=20°.则∠CDE= ,∠DEB= .
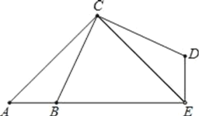
【答案】(1)C点;∠ACE或∠BCD;90度;(2)△CAB和△CED全等;(3)115°,90°.
【解析】
(1)利用旋转的定义求解;
(2)根据旋转的性质进行判断;
(3)先利用等腰直角三角形的性质得∠A=∠CEA=45°,则根据三角形内角和可计算出∠ABC=115°,再根据旋转的性质得∠CDE=∠ABC=115°,∠CED=∠A=45°,从而得到∠DEB=90°.
(1)旋转中心是C点;旋转角为∠ACE或∠BCD;旋转了90度;
(2)图中△CAB和△CED全等;
(3)∵△ACE是等腰直角三角形,∠ACE=90°,
∴∠A=∠CEA=45°.
∵∠ACB=20°,
∴∠ABC=180°﹣45°﹣20°=115°.
∵△CAB经过逆时针旋转后到达△CED的位置,
∴∠CDE=∠ABC=115°,∠CED=∠A=45°,
∴∠DEB=45°+45°=90°.
故答案为:115°,90°.


科目:初中数学 来源: 题型:
【题目】某厂共有120名生产工人,每个工人每天可生产螺栓25个或螺母20个,如果一个螺栓与两个螺母配成一套 ,那么每天安排多名工人生产螺栓,多少名工人生产螺母,才能使每天生产出来的产品配成最多套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)如图1,求证∠BAC=∠B+2∠E;
(2)如图2,过点A作AF⊥BC,垂足为点F,若∠DCE=2∠CAF,∠B=2∠E,求∠BAC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字1,2,3,4,B布袋中有三个除标号外完全相同的小球,小球上分别标有数字2,4,6.小明先从A布袋中随机取出﹣个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)若用(m,n)表示小明取球时m与n 的对应值,请画出树形图或列表写出(m,n)的所有取值;
(2)求关于x的一元二次方程x2﹣mx+![]() n=0有实数根的概率.
n=0有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(m﹣1)x2﹣x﹣2=0.
(1)若x=﹣1是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有实数根;
(3)若x1,x2是方程的两个根,且![]() ,试求实数m的值.
,试求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(a﹣1)x2+2x+a﹣1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
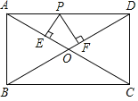
【题目】已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系![]() 的原点O在格点上,
的原点O在格点上, ![]() 轴、
轴、![]() 轴都在网格线上.线段AB的端点A、B在格点上.
轴都在网格线上.线段AB的端点A、B在格点上.

(1)将线段AB绕点O逆时针90°得到线段A1B1,请在图中画出线段A1B1;
(2)在(1)的条件下,线段A2B2与线段A1B1关于原点O成中心对称,请在图中画出线段A2B2;
(3)在(1)、(2)的条件下,点P是此平面直角坐标系内的一点,当以点A、B、B2、P为顶点的四边形是平行四边形时,请直接写出点P的坐标: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方
向依次不断移动,每次移动1个单位,其行走路线如下图所示.

(1)填写下列各点的坐标:A4( , )、A8( , )、A12( , );
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com