
【题目】已知关于x的方程(a﹣1)x2+2x+a﹣1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
【答案】(1)a=![]() ,方程的另一根为
,方程的另一根为![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)把![]() 代入方程,求出
代入方程,求出![]() 的值,再把
的值,再把![]() 代入原方程,进一步解方程即可;
代入原方程,进一步解方程即可;
(2)分两种情况探讨:①当![]() 时,为一元一次方程;②当
时,为一元一次方程;②当![]() 时,利用
时,利用![]() 求出
求出![]() 的值,再代入解方程即可.
的值,再代入解方程即可.
试题解析:(1)将x=2代入方程(a-1)x2+2x+a-1=0,解得:a=![]() .
.
将a=![]() 代入原方程得-
代入原方程得-![]() x2+2x-
x2+2x-![]() =0,解得:
=0,解得: ![]()
∴a=![]() ,方程的另一根为
,方程的另一根为![]()
(2)①当a=1时,方程为2x=0,解得:x=0
②当a≠1时,由b2-4ac=0得4-4(a-1)2=0
解得:a=2或0.
当a=2时, 原方程为:x2+2x+1=0,解得: ![]()
当a=0时, 原方程为:-x2+2x-1=0,解得: ![]() =
=![]() =1.
=1.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的平分线与BC的中垂线DE交于点E,过点E作AC边的垂线,垂足为N,过点E作AB延长线的垂线,垂足为M.
(1)求证:BM=CN;
(2)若,AB=2,AC=8,求BM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

(1)作出△ABC绕点A逆时针旋转90°的△A1B1C1;作出△ABC关于原点O成中心对称的△A2B2C2;
(2)点B1的坐标为__________,点C2的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ACE是等腰直角三角形,∠ACE=90°,B点为AE上一点,△CAB经过逆时针旋转后到达△CED的位置.
问:(1)旋转中心是哪个点?旋转角是哪个角?旋转了多少度?
(2)图中哪两个三角形全等?
(3)若∠ACB=20°.则∠CDE= ,∠DEB= .
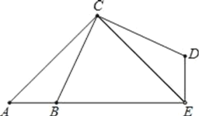
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电子产品共4件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品________件;
(2)如果从中任意取出2件,利用列表或树状图求取出2件都是正品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H.点G在⊙O上,过点G作直线EF,交CD延长线于点E,交AB的延长线于点F.连接AG交CD于K,且KE=GE.

(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若AC∥EF,![]() ,FB=1,求⊙O的半径.
,FB=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AC=5,AB=12,∠BAC的平分线与BC的垂直平分线DG交于点D,DE⊥AC的延长线于点E,DF⊥AB于点F.

(1)求证:CE=BF;
(2)求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地面公交和共享单车的发展,“公交车+单车”的方式已成为很多市民出行的选择。小明放学后从寿春中学出发,先乘坐公交车,根据路面交通的拥堵的实际情况,灵活决定在离家较近的A、B、C、D、E中的某一公交站下车,再骑共享单车回家,设他乘公交车的时间y1(单位:分钟)与下车站点到学校距离x(3≤x≤5)(单位:千米)之间函数关系为y1=2x+2,小明骑单车的时间y2(单位:分钟)与x(3≤x≤5)之间的满足二次函数关系,其具体对应值如下表所示:
地铁站 | A | B | C | D | E |
X(千米) | 3 |
| 4 |
| 5 |
Y2(分钟) | 11 |
| 6 |
| 3 |
(1)求y2关于x的函数表达式;
(2)求小明从学校回到家的时间y(单位:分钟)与x的函数表达式;
(3)请通过计算说明:小明应选择在哪一站下公交车,才能使他从学校回家所需的时间最短?并求出最短时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com