
|


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
| A、原来奥运会纪录是175公斤 |
| B、原来奥运会纪录是77公斤 |
| C、原来奥运会纪录小于77公斤 |
| D、原来奥运会纪录小于175公斤 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 黄河游览区在假日一周旅游的调查中每天旅游的人数变化如表(正数表示比前一天多的人数,负数表示比前一天少的人数):
黄河游览区在假日一周旅游的调查中每天旅游的人数变化如表(正数表示比前一天多的人数,负数表示比前一天少的人数):| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化单位万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
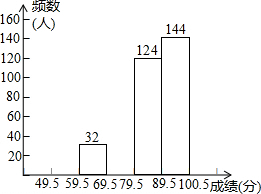 某市七年级有10000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分进行统计请你根据不完整的频率分布表.解答下列问题:
某市七年级有10000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分进行统计请你根据不完整的频率分布表.解答下列问题:| 分 组 | 频 数 | 频 率 |
| 49.5~59.5 | 20 | a |
| 59.5~69.5 | 32 | 0.08 |
| 69.5~79.5 | b | 0.20 |
| 79.5~89.5 | 124 | 0.31 |
| 89.5~100.5 | 144 | 0.36 |
| 合 计 | 400 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
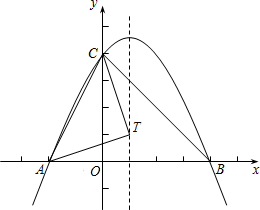 如图,抛物线y=ax2+bx+4(a≠0)与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C.
如图,抛物线y=ax2+bx+4(a≠0)与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C.| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
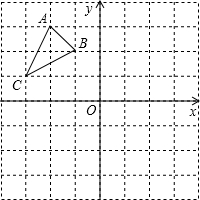 如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.
如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:
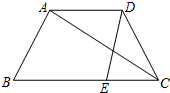 如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.
如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.| AD |
| DC |
| AB |
| AC |
| AD |
| DC |
| CE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com