
| A. | 24个交点 | B. | 36个交点 | C. | 45个交点 | D. | 55个交点 |
分析 在同一平面内,直线相交时得到最多交点的方法是:每增加一条直线这条直线都要与之前的所有线段相交,即第n条直线时交点最多有1+2+3+4+…+(n-1)个,整理即可得到一般规律:$\frac{n(n-1)}{2}$,再把特殊值n=10代入即可求解.
解答 解:在同一平面内,两条直线相交时最多有1个交点,三条直线最多有3=1+2个交点,四条直线最多有6=1+2+3个交点,…,n条直线最多有1+2+3+4+…+(n-1)个交点,即1+2+3+4+…+(n-1)=$\frac{n(n-1)}{2}$.
当n=10时,$\frac{10(10-1)}{2}$=$\frac{90}{2}$=45
故选:C.
点评 本题主要考查直线的交点问题.注意直线相交时得到最多交点的方法是:每增加一条直线,这条直线都要与之前的所有线段相交.


科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).
在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
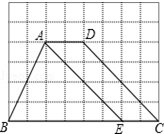 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=5 | B. | a=-5 | C. | a=$\frac{1}{5}$ | D. | a=-$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $x-\frac{1}{2}y$ | B. | $\frac{3}{7}x$ | C. | $\frac{1}{x-1}$ | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3×105 | B. | 3×106 | C. | 3×104 | D. | 30×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
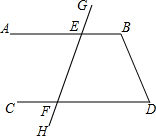 请补全证明过程.如图,已知线段AB,CD与GH相交于点E,F,∠GEB=?,∠EFD=β,∠D=50°,求∠B的度数.
请补全证明过程.如图,已知线段AB,CD与GH相交于点E,F,∠GEB=?,∠EFD=β,∠D=50°,求∠B的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com