
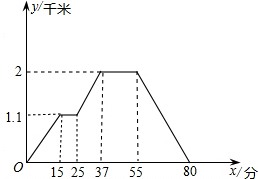
 如图的图象反映的过程是:小明从家去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:
如图的图象反映的过程是:小明从家去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:| 2 | ||
|


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
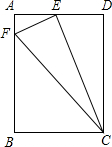 如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE).
如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE).| AB |
| BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
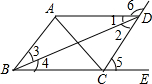 如图,∠5=∠CDA=∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:
如图,∠5=∠CDA=∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:查看答案和解析>>
科目:初中数学 来源: 题型:
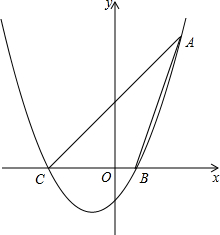 如图,已知二次函数y=
如图,已知二次函数y=| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com