
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
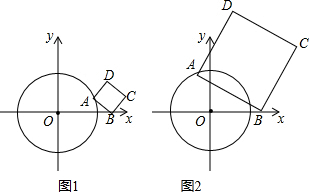
 解:(1)如图1,∵⊙O的半径为
解:(1)如图1,∵⊙O的半径为| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |

| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| OB2-BM2 |
| ||
| 2 |
| 3 |
| OP2-OM2 |
| ||
| 2 |
| 5 |


科目:初中数学 来源: 题型:
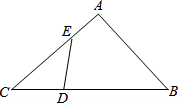 已知:如图,△ABC中,点D、E分别是BC、AC边上的点,且BC:DC=3:1,∠B=∠CED,BC=12,AC=8.
已知:如图,△ABC中,点D、E分别是BC、AC边上的点,且BC:DC=3:1,∠B=∠CED,BC=12,AC=8.| AB |
| a |
| AC |
| b |
| a |
| b |
| DE |
查看答案和解析>>
科目:初中数学 来源: 题型:
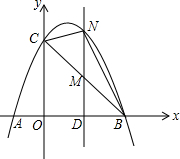 如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点.
如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点.查看答案和解析>>
科目:初中数学 来源: 题型:
 在海洋上有一近似于四边形的岛屿,其平面图如图,小明据此构造出该岛的一个数学模型(如图四边形ABCD)来求岛屿的面积,其中∠A=∠D=90°,AB=BC=15千米,CD=3
在海洋上有一近似于四边形的岛屿,其平面图如图,小明据此构造出该岛的一个数学模型(如图四边形ABCD)来求岛屿的面积,其中∠A=∠D=90°,AB=BC=15千米,CD=3| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
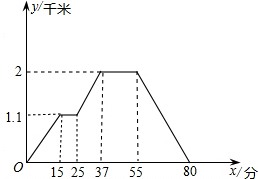 如图的图象反映的过程是:小明从家去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:
如图的图象反映的过程是:小明从家去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
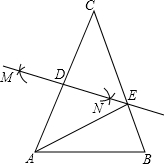 如图,在△ABC中,AC=BC,∠B=70°,分别以点A、C为圆心,大于
如图,在△ABC中,AC=BC,∠B=70°,分别以点A、C为圆心,大于| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com