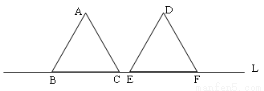
边长为2的等边△ABC与等边△DEF互相重合，将△ABC沿直线L向左平移m个单位长度，将△DEF向右也平移m个单位长度，如图，当C、E是线段BF的三等分点时，m的值为__ ．
名校课堂系列答案科目：初中数学 来源：2016届江苏省句容市九年级下学期竞赛数学试卷（解析版） 题型：解答题
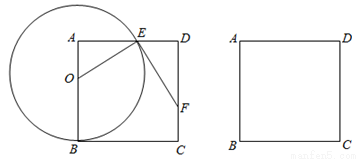
如图，已知：正方形ABCD中，AB=8，点O为边AB上一动点，以点O为圆心，OB为半径的⊙O交边AD于点E（不与点A、D重合），EF⊥OE交边CD于点F．设BO=x，AE=y．
（1）求y关于x的函数关系式，并写出x的取值范围；
（2）在点O运动的过程中，△EFD的周长是否发生变化？如果发生变化，请用x的代数式表示△EFD的周长；如果不变化，请求出△EFD的周长；
（3）以点A为圆心，OA为半径作圆，在点O运动的过程中，讨论⊙O与⊙A的位置关系，并写出相应的x的取值范围．
查看答案和解析>>
科目：初中数学 来源：2016届江苏省句容市九年级下学期竞赛数学试卷（解析版） 题型：单选题
在某校“我的梦想”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（ ）.
A. 众数 B. 中位数 C. 平均数 D. 方差
查看答案和解析>>
科目：初中数学 来源：2016-2017学年江苏省无锡市天一实验学校七年级下学期期中考试数学试卷（解析版） 题型：解答题
请将下列证明过程补充完整：
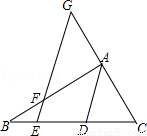
已知：如图，AD是△ABC的角平分线，点E在BC上，点G在CA的延长线上，EG交AB于点F，且∠BEF+∠ADC=180°．
求证：∠AFG=∠G．
证明：∵∠BEF+∠ADC=180°（已知），
又∵ （平角的定义），
∴∠GED=∠ADC（ ），
∴AD∥GE（ ），
∴∠AFG=∠BAD（ ），
且∠G=∠CAD（ ），
∵AD是△ABC的角平分线（已知），
∴∠BAD=∠CAD（角平分线的定义），
∴∠AFG=∠G（ ）．
查看答案和解析>>
科目：初中数学 来源：2016-2017学年江苏省无锡市天一实验学校七年级下学期期中考试数学试卷（解析版） 题型：填空题
若32÷8n-1=2n，则n=_____________．
查看答案和解析>>
科目：初中数学 来源：2016-2017学年江苏省无锡市天一实验学校七年级下学期期中考试数学试卷（解析版） 题型：选择题
已知一个多边形的内角和是外角和的4倍，则这个多边形
A.八边形 B.十二边形 C. 十边形 D. 九边形
查看答案和解析>>
科目：初中数学 来源：2017届内蒙古牙克石市九年级5月毕业生学业水平模拟测试数学试卷（解析版） 题型：填空题
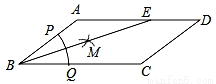
如图，在□ABCD中，AB=3，BC=5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心以大于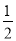
PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为_____________．
查看答案和解析>>
科目：初中数学 来源：[首发]2016-2017学年广西桂林市八年级下学期期中质量检测数学试卷（解析版） 题型：解答题
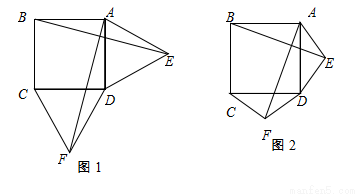
如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF，BE.
（1）请写出AF与BE的数量关系与位置关系分别是什么，并证明.
（2）如图2，若将条件“两个等边三角形ADE和DCF”变为两个等腰三角形ADE和DCF，且EA=ED=FD=FC，第（1）问中的结论是否仍然成立?请作出判断并给予证明；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=______.