
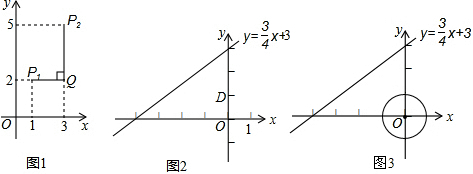
分析 (1)①根据题意,设点B的坐标是(0,b),根据点A与点B的“非常距离”为2,可得|0-b|=2,据此求出b的值,即可求出满足条件的点B的坐标.
②根据题意,设点B的坐标是(0,b),判断出当|b|≤$\frac{1}{2}$时,点A与点B的“非常距离”的最小值是$\frac{1}{2}$即可.
(2)①设点C的坐标是(a,$\frac{3}{4}a+3$),分三种情况讨论:Ⅰ、当a≥0时;Ⅱ、当a≤-4时;Ⅲ、当-4<a<0时;求出点C与点D的“非常距离”的最小值及相应的点C的坐标即可.
②设点C的坐标是(a,$\frac{3}{4}a+3$),分三种情况讨论:Ⅰ、当a≥0时;Ⅱ、当a≤-4时;Ⅲ、当-4<a<0时;判断出当点E在过原点且与直线y=$\frac{3}{4}$x+3垂直的直线上时,点C与点E的“非常距离”最小,据此求出点C与点D的“非常距离”的最小值及相应的点E和点C的坐标即可.
解答 解:(1)①∵B为y轴上的一个动点,
∴设点B的坐标是(0,b),
∵点A与点B的“非常距离”为2,|-$\frac{1}{2}$-0|=$\frac{1}{2}$,
∴|0-b|=2,
解得b=2或b=-2,
∴满足条件的点B的坐标是(0,-2)或(0,2).
②∵B为y轴上的一个动点,
∴设点B的坐标是(0,b),
∵|-$\frac{1}{2}$-0|=$\frac{1}{2}$,
∴当|b|≤$\frac{1}{2}$时,点A与点B的“非常距离”的最小值是$\frac{1}{2}$.
(2)①如图2,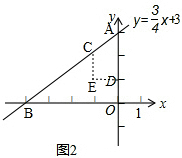 ,
,
设点C的坐标是(a,$\frac{3}{4}a+3$),
Ⅰ、当a≥0时,
∵点A的坐标是(0,3),点D的坐标是(0,1),
∴点C与点D的“非常距离”的最小值是:|3-1|=2;
Ⅱ、当a≤-4时,
∵点B的坐标是(-4,0),点D的坐标是(0,1),
∴点C与点D的“非常距离”的最小值是:|-4|=4;
Ⅲ、当-4<a<0时,
当CE=DE时,点C与点D的“非常距离”最小,
此时$\frac{3}{4}a+3$-1=-a,
解得a=-$\frac{8}{7}$,
∴$\frac{3}{4}a+3$=$\frac{3}{4}×(-\frac{8}{7})+3=\frac{15}{7}$,
∴点C与点D的“非常距离”的最小值是$\frac{8}{7}$,点C的坐标是(-$\frac{8}{7}$,$\frac{15}{7}$).
综上,可得
点C与点D的“非常距离”的最小值是$\frac{8}{7}$,点C的坐标是(-$\frac{8}{7}$,$\frac{15}{7}$).
②如图3,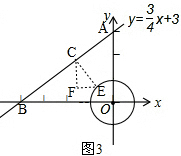 ,
,
设点C的坐标是(a,$\frac{3}{4}a+3$),点E的坐标是(x,y),
Ⅰ、当c≥0时,
∵点A的坐标是(0,3),圆与y轴的正半轴交点的坐标是(0,1),
∴点C与点D的“非常距离”的最小值是:|3-1|=2;
Ⅱ、当c≤-4时,
∵点B的坐标是(-4,0),圆与x轴的负半轴交点的坐标是(-1,0),
∴点C与点D的“非常距离”的最小值是:|-4-(-1)|=3;
Ⅲ、当-4<a<0时,
当点E在过原点且与直线y=$\frac{3}{4}$x+3垂直的直线上时,点C与点E的“非常距离”最小,
∴$\left\{\begin{array}{l}{\frac{y}{x}=-\frac{4}{3}}\\{{x}^{2}{+y}^{2}=1}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=-\frac{3}{5}}\\{y=\frac{4}{5}}\end{array}\right.$
由$\frac{3}{4}a+3$-$\frac{4}{5}$=-$\frac{3}{5}-a$,
解得a=-$\frac{8}{5}$,
∴$\frac{3}{4}a+3$=$\frac{3}{4}×(-\frac{8}{5})+3=\frac{9}{5}$,
∵$\frac{9}{5}-\frac{4}{5}=1$,
∴点C与点D的“非常距离”的最小值是1,点E的坐标是(-$\frac{3}{5}$,$\frac{4}{5}$),点C的坐标是(-$\frac{8}{5}$,$\frac{9}{5}$).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了对“非常距离”的含义的理解,要熟练掌握,并能求出两点之间的“非常距离”.


科目:初中数学 来源: 题型:选择题
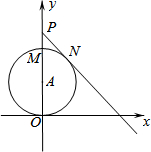 如图,直角坐标系中,P点坐标为(0,4),M为线段OP上(不含O、P)一动点,以OM为直径作⊙A,PN切⊙A于N,设PN-PM=m,则m的值( )
如图,直角坐标系中,P点坐标为(0,4),M为线段OP上(不含O、P)一动点,以OM为直径作⊙A,PN切⊙A于N,设PN-PM=m,则m的值( )| A. | 为定值1 | B. | 0<m≤1 | C. | 0<m≤2 | D. | $\frac{1}{2}$≤m≤1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 | 70 | |
| 英语 | 88 | 82 | 94 | 85 | 76 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
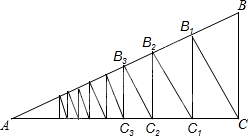 如图,在Rt△ABC中,BC⊥AC,∠BAC=30°,CB1⊥AB,B1C1⊥AC,C1B2⊥AB,B2C2⊥AC…以此类推,若BC=a,则BnCn=($\frac{3}{4}$)na.
如图,在Rt△ABC中,BC⊥AC,∠BAC=30°,CB1⊥AB,B1C1⊥AC,C1B2⊥AB,B2C2⊥AC…以此类推,若BC=a,则BnCn=($\frac{3}{4}$)na.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.8米 | B. | 64米 | C. | 9.6米 | D. | 2.4米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com