
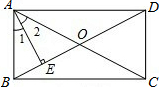
 如图,矩形ABCD的对角线AC、BD相交于点O,AE⊥BD,垂足为E,∠1=∠2,AB=2cm.
如图,矩形ABCD的对角线AC、BD相交于点O,AE⊥BD,垂足为E,∠1=∠2,AB=2cm.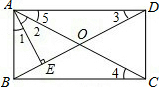 解:(1)如图,在矩形ABCD中,∠BAD=90°,∠3=∠4=∠5
解:(1)如图,在矩形ABCD中,∠BAD=90°,∠3=∠4=∠5| 3 |
| 3 |


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
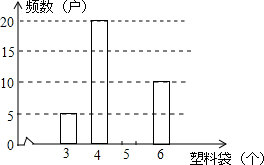 为了了解某居民区10000户家庭丢弃废旧塑料袋的情况,某环保组织在今年6月5日(世界环境日)这一天随机抽样调查了该小区50户家庭丢弃塑料袋的情况,制成如下统计表和条形统计图(如图)(均不完整).
为了了解某居民区10000户家庭丢弃废旧塑料袋的情况,某环保组织在今年6月5日(世界环境日)这一天随机抽样调查了该小区50户家庭丢弃塑料袋的情况,制成如下统计表和条形统计图(如图)(均不完整).| 每户丢弃废旧塑料袋(个) | 频数(户) | 频率 |
| 3 | 5 | 0.1 |
| 4 | 20 | 0.4 |
| 5 | ||
| 6 | 10 | 0.2 |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AB |
| 1 |
| 3 |
| OM |
| NE |
| OM |
| OD |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com