



 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
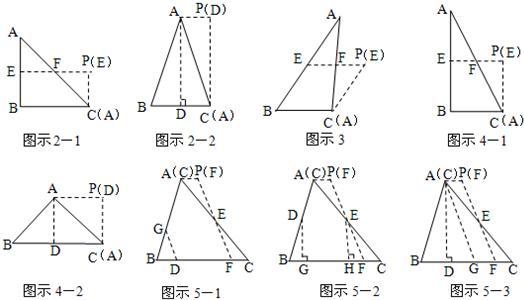
 23、在△ABC中,借助作图工具可以作出中位线EF,沿着中位线EF一刀剪切后,用得到的△AEF和四边形EBCF可以拼接成平行四边形EBCP,剪切线与拼图过程如图所示,依照上述方法,按要求完成下列操作设计,并画出图形说明.
23、在△ABC中,借助作图工具可以作出中位线EF,沿着中位线EF一刀剪切后,用得到的△AEF和四边形EBCF可以拼接成平行四边形EBCP,剪切线与拼图过程如图所示,依照上述方法,按要求完成下列操作设计,并画出图形说明.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
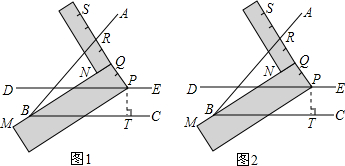 (1)阅读理解:
(1)阅读理解: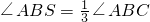 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出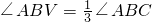 (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com