Question

【题目】在矩形ABCD中，AD=2AB=4，E是AD的中点，一块足够大的三角板的直角顶点与点E重合，将三角板绕点E旋转，三角板的两直角边分别交AB，BC（或它们的延长线）于点M，N．

（1）观察图1，直接写出∠AEM与∠BNE的关系是；（不用证明）
（2）如图1，当M、N都分别在AB、BC上时，可探究出BN与AM的关系为：；（不用证明）
（3）如图2，当M、N都分别在AB、BC的延长线上时，（2）中BN与AM的关系式是否仍然成立？若成立，请说明理由：若不成立，写出你认为成立的结论，并说明理由．

Answer 1

【答案】
（1）∠AEM+∠BNE=90°
（2）BN⊥AM，BN﹣AM=2
（3）

解：当M、N都分别在AB、BC的延长线上时，（2）中BN与AM的关系式仍然成立．

证明：如图2，

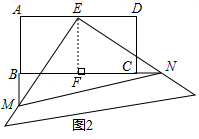
∵四边形ABCD为矩形，

∴BN⊥AM，

过E作EF⊥BC于F

∵矩形ABCD中，AD=2AB=4，E是AD的中点，

∴AE=EF=AB=BF=2，

∵∠AEM+∠MEF=90°，∠NEF+∠MEF=90°，

∴∠AEM=∠FEN，

，

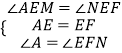∴Rt△AEM≌Rt△FEN，

∴AM=FN，

∴BN﹣AM=BN﹣FN=BF=2．

【解析】解：（1.）∵四边形ABCD为矩形，
∴AD∥BC，
∴∠DEN=∠BNE，
∵∠MEN=90°，
∴∠AEM+∠DEN=90°，
∴∠AEM+∠BNE=90°，
故答案为：∠AEM+∠BNE=90°；
（2.）BN⊥AM，BN﹣AM=2；
证明：如图1，∵四边形ABCD为矩形，
∴BN⊥AM，
过E作EF⊥BC于F，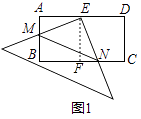

∵矩形ABCD中，AD=2AB=4，E是AD的中点
∴AE=EF=AB=BF=2，
∵∠AEM+∠MEF=90°，∠NEF+∠MEF=90°，
∴∠AEM=∠NEF，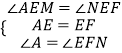
，
∴Rt△AEM≌Rt△FEN，
∴AM=FN，
∴BN﹣AM=BN﹣FN=BF=2；
故答案为：BN⊥AM，BN﹣AM=2；
（1）由矩形的性质可得AD∥BC，由平行线的性质定理可得∠DEN=∠BNE，由∠MEN=90°，易得∠AEM+∠DEN=90°，可得∠AEM+∠BNE=90°；（2）由矩形的性质可得BN⊥AM，过E作EF⊥BC于F，由E是AD的中点可得，AD=2AB=4，易得AE=EF，易得Rt△AEM≌Rt△FEN，由全等三角形的性质可得AM=FN，易得BN﹣AM=BN﹣FN=BF=2；（3）同（2）可证得结论．