
ЎѕМвДїЎїРЈіµ°ІИ«КЗЅьјёДкЙз»б№ШЧўµДЦШґуОКМвЈ¬°ІИ«Тю»јЦчТЄКЗі¬ЛЩєНі¬ФШЈ®ДіЦРС§КэС§»о¶ЇРЎЧйЙијЖБЛИзПВјмІв№«В·ЙПРРК»µДЖыіµЛЩ¶ИµДКµСйЈєПИФЪ№«В·ЕФ±ЯСЎИЎТ»µгCЈ¬ФЩФЪ±КЦ±µДіµµАLЙПИ·¶ЁµгDЈ¬К№CDУлLґ№Ц±Ј¬ІвµГCDµДі¤µИУЪ24ГЧЈ¬ФЪLЙПµгDµДН¬ІаИЎµгAЎўBЈ¬К№ЎПCAD=30ЎгЈ¬ЎПCBD=60ЎгЈ® 
ЈЁ1Ј©ЗуABµДі¤ЈЁЅб№ы±ЈБфёщєЕЈ©Ј»
ЈЁ2Ј©ТСЦЄ±ѕВ·¶О¶ФРЈіµПЮЛЩОЄ45З§ГЧ/РЎК±Ј¬ИфІвµГДіБѕРЈіµґУAµЅBУГК±2ГлЈ¬ХвБѕРЈіµКЗ·сі¬ЛЩЈїЛµГчАнУЙЈ®ЈЁІОїјКэѕЭЈє ![]() ЎЦ1.73Ј¬
ЎЦ1.73Ј¬ ![]() ЎЦ1.41Ј©
ЎЦ1.41Ј©
Ўѕґр°ёЎї
ЈЁ1Ј©ЅвЈєУЙо}ТвµГЈ¬
ФЪRtЎчADCЦРЈ¬AD= ![]() =
= ![]() =24
=24 ![]() ЎЦ36.33ЈЁГЧЈ©Ј¬
ЎЦ36.33ЈЁГЧЈ©Ј¬
ФЪRtЎчBDCЦРЈ¬BD= ![]() =
= ![]() =8
=8 ![]() Ј¬
Ј¬
ФтAB=AD©ЃBD=16 ![]() Ј»
Ј»
ЈЁ2Ј©ЅвЈєі¬ЛЩЈ®
АнУЙЈєЎЯЖыіµґУAµЅBУГК±2ГлЈ¬
ЎаЛЩ¶ИОЄ16ЎБ1.73ЎВ2=13.84ГЧ/Гл
13.84ЎБ3.6=49.824З§ГЧ/К±Јѕ45З§ГЧ/РЎК±Ј®
ЎаґЛРЈіµФЪABВ·¶Оі¬ЛЩЈ®
ЎѕЅвОцЎїЈЁ1Ј©·Ц±рФЪRtЎчADCУлRtЎчBDCЦРЈ¬АыУГХэЗРєЇКэЈ¬јґїЙЗуµГADУлBDµДі¤Ј¬јМ¶шЗуµГABµДі¤Ј»ЈЁ2Ј©УЙґУAµЅBУГК±2ГлЈ¬јґїЙЗуµГХвБѕРЈіµµДЛЩ¶ИЈ¬±ИЅПУл40З§ГЧ/РЎК±µДґуРЎЈ¬јґїЙИ·¶ЁХвБѕРЈіµКЗ·сі¬ЛЩЈ®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪѕШРОABCDЦРЈ¬AD=2AB=4Ј¬EКЗADµДЦРµгЈ¬Т»їйЧг№»ґуµДИэЅЗ°еµДЦ±ЅЗ¶ҐµгУлµгEЦШєПЈ¬Ѕ«ИэЅЗ°еИЖµгEРэЧЄЈ¬ИэЅЗ°еµДБЅЦ±ЅЗ±Я·Ц±рЅ»ABЈ¬BCЈЁ»тЛьГЗµДСУі¤ПЯЈ©УЪµгMЈ¬NЈ®
ЈЁ1Ј©№ЫІмНј1Ј¬Ц±ЅУРґіцЎПAEMУлЎПBNEµД№ШПµКЗЈ»ЈЁІ»УГЦ¤ГчЈ©
ЈЁ2Ј©ИзНј1Ј¬µ±MЎўN¶ј·Ц±рФЪABЎўBCЙПК±Ј¬їЙМЅѕїіцBNУлAMµД№ШПµОЄЈєЈ»ЈЁІ»УГЦ¤ГчЈ©
ЈЁ3Ј©ИзНј2Ј¬µ±MЎўN¶ј·Ц±рФЪABЎўBCµДСУі¤ПЯЙПК±Ј¬ЈЁ2Ј©ЦРBNУлAMµД№ШПµКЅКЗ·сИФИ»іЙБўЈїИфіЙБўЈ¬ЗлЛµГчАнУЙЈєИфІ»іЙБўЈ¬РґіцДгИПОЄіЙБўµДЅбВЫЈ¬ІўЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪ![]() ЦРЈ¬
ЦРЈ¬ ![]() Ј¬µг
Ј¬µг![]() КЗЦ±ПЯ
КЗЦ±ПЯ![]() ЙПТ»µгЈЁІ»Ул
ЙПТ»µгЈЁІ»Ул![]() ЦШєПЈ©Ј¬ТФ
ЦШєПЈ©Ј¬ТФ![]() ОЄТ»±ЯФЪ
ОЄТ»±ЯФЪ![]() µДУТІаЧч
µДУТІаЧч![]() Ј¬К№
Ј¬К№![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ј®
Ј®
ЈЁ1Ј©ИзНј1Ј¬µ±µг![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈ¬Из№ы
ЙПЈ¬Из№ы![]() Ј¬Фт
Ј¬Фт![]() ¶ИЈ»
¶ИЈ»
ЈЁ2Ј©Йи![]() Ј¬
Ј¬ ![]() Ј®
Ј®
ўЩИзНј2Ј¬µ±µг![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПТЖ¶ЇЈ¬Фт
ЙПТЖ¶ЇЈ¬Фт![]() Ц®јдУРФхСщµДКэБї№ШПµЈїЗлЛµГчАнУЙЈ»
Ц®јдУРФхСщµДКэБї№ШПµЈїЗлЛµГчАнУЙЈ»
ўЪµ±µг![]() ФЪЦ±ПЯ
ФЪЦ±ПЯ![]() ЙПТЖ¶ЇЈ¬Фт
ЙПТЖ¶ЇЈ¬Фт![]() Ц®јдУРФхСщµДКэБї№ШПµЈїЗл»іцНјРОІўЦ±ЅУРґіцПаУ¦µДЅбВЫЈ®
Ц®јдУРФхСщµДКэБї№ШПµЈїЗл»іцНјРОІўЦ±ЅУРґіцПаУ¦µДЅбВЫЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОТГЗУГ[a]±нКѕІ»ґуУЪaµДЧоґуХыКэЈ¬АэИзЈє[2.5]ЈЅ2Ј¬[3]ЈЅ3Ј¬[Ј2.5]ЈЅЈ3Ј»УГ<a>±нКѕґуУЪaµДЧоРЎХыКэЈ¬АэИзЈє<2.5>ЈЅ3Ј¬<4>ЈЅ5Ј¬<Ј1.5>ЈЅЈ1.
ЅвѕцПВБРОКМвЈє
ЈЁ1Ј©[Ј4.5]ЈЅ___Ј¬<3.5>ЈЅ___Ј»
ЈЁ2Ј©Иф[x]ЈЅ2Ј¬ФтxµДИЎЦµ·¶О§КЗ___Ј»Иф<y>ЈЅЈ1Ј¬ФтyµДИЎЦµ·¶О§КЗ___.
ЈЁ3Ј©ТСЦЄxЈ¬yВъЧг·ЅіМЧй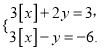 ЗуxЈ¬yµДИЎЦµ·¶О§.
ЗуxЈ¬yµДИЎЦµ·¶О§.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЅсДк4ФВЈ¬ОТКРДіЦРС§ѕЩРРБЛЎ°°®ОТЦР№ъАКЛР±ИИьЎ±»о¶ЇЈ¬ёщѕЭС§ЙъµДіЙјЁ»®·ЦОЄAЎўBЎўCЎўDЛДёцµИј¶Ј¬Іў»жЦЖБЛИзПВБЅЦЦІ»НкХыµДНіјЖНјЈ®ёщѕЭНјЦРМṩµДРЕПўЈ¬»ШґрПВБРОКМвЈє
ЈЁ1Ј©ІОјУАКЛР±ИИьµДС§Йъ№ІУРИЛЈ¬Іў°СМхРОНіјЖНјІ№ідНкХыЈ»
ЈЁ2Ј©ЙИРОНіјЖНјЦРЈ¬m= Ј¬ n=Ј»CµИј¶¶ФУ¦ЙИРОµДФІРДЅЗОЄ¶ИЈ»
ЈЁ3Ј©С§РЈЧј±ёґУ»сAµИј¶µДС§ЙъЦРЛж»ъСЎИЎ2ИЛЈ¬ІОјУКРѕЩ°мµДАКЛР±ИИьЈ¬ЗлАыУГБР±н·Ё»тКчРОНј·ЁЈ¬Зу»сAµИј¶µДРЎГчІОјУКРАКЛР±ИИьµДёЕВКЈ® 
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ѕШРОABCDЦРЈ¬AB=4Ј¬BC=2Ј¬EКЗABµДЦРµгЈ¬Ц±ПЯlЖЅРРУЪЦ±ПЯECЈ¬ЗТЦ±ПЯlУлЦ±ПЯECЦ®јдµДѕаАлОЄ2Ј¬µгFФЪѕШРОABCD±ЯЙПЈ¬Ѕ«ѕШРОABCDСШЦ±ПЯEFХЫµюЈ¬К№µгAЗЎєГВдФЪЦ±ПЯlЙПЈ¬ФтDFµДі¤ОЄ Ј® 
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї»іцєЇКэ![]() µДНјПу.
µДНјПу.
ЈЁ1Ј©єЇКэ![]() µДЧФ±дБїxµДИЎЦµ·¶О§КЗ________Ј»
µДЧФ±дБїxµДИЎЦµ·¶О§КЗ________Ј»
ЈЁ2Ј©БР±нЈЁ°С±нёсІ№ідНкХыЈ©
x | ЎЎ | -2 | -1 | 0 | 1 | 2 | 3 | 4 | ЎЎ |
y |
ЈЁ3Ј©ГиµгЎўБ¬ПЯ
ЈЁ4Ј©ЅбєПНјПуЈ¬РґіцєЇКэµДТ»МхРФЦК________________________________________.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїХэКэxµДБЅёцЖЅ·Ѕёщ·Ц±рОЄ3©ЃaєН2a+7Ј¬Фт44©ЃxµДБў·ЅёщОЄЈЁЎЎЎЎЈ©
A.©Ѓ5B.5C.13D.10
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ№ШУЪxµДТ»ФЄ¶юґО·ЅіМ![]() .ЈЁЖдЦРmОЄКµКэЈ©
.ЈЁЖдЦРmОЄКµКэЈ©
ЈЁ1Ј©ИфґЛ·ЅіМµДТ»ёц·ЗБгКµКэёщОЄkЈ¬
ўЩ µ±k = mК±Ј¬ЗуmµДЦµЈ»
ўЪ ИфјЗ![]() ОЄyЈ¬ЗуyУлmµД№ШПµКЅЈ»
ОЄyЈ¬ЗуyУлmµД№ШПµКЅЈ»
ЈЁ2Ј©µ±![]() ЈјmЈј2К±Ј¬ЕР¶ПґЛ·ЅіМµДКµКэёщµДёцКэІўЛµГчАнУЙ
ЈјmЈј2К±Ј¬ЕР¶ПґЛ·ЅіМµДКµКэёщµДёцКэІўЛµГчАнУЙ
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com