
【题目】如图,△ABC中,∠ABC和∠ACB的角平分线BE、CF相交于点I,

(1)∠BIC=120°,求∠A的度数
(2)当∠BIC=135°,则∠A= 。
(3)请你用数学表达式归纳出∠BIC与∠A的关系式,并说明理由。
【答案】(1)60° (2)120° (3)∠BIC=90°+![]() ∠A.或∠A =2∠BIC - 180°
∠A.或∠A =2∠BIC - 180°
【解析】试题(1)根据题目给出的数据,可以知道∠A=![]() ;(2)总结上述的规律可得出∠A的值;(3)根据三角形的内角和定理用 ∠A表示出
;(2)总结上述的规律可得出∠A的值;(3)根据三角形的内角和定理用 ∠A表示出
∠ABC+∠ACB,再根据角平分线的定义表示出∠IEC+∠ICE,然后再利用三角形内角和定理即可得出结论.
试题解析:
(1)由题意得,∵∠BIC是△CEI的外角,
∴∠BIC=∠IEC+∠ICE(三角形外角定理),
∵∠IEC是△ABE的外角,
∴∠IDC=∠A+∠ABD(三角形外角定理),
∵BI、CI是∠ABC、∠ACB的平分线,
∴∠ABE=![]() ∠ABC,∠ICE=
∠ABC,∠ICE=![]() ∠ACB(角平分线定义),
∠ACB(角平分线定义),
∴∠BIC=![]() (∠ABC+∠ACB)+∠A=
(∠ABC+∠ACB)+∠A=![]() (
(![]() ∠A)+∠A=
∠A)+∠A=![]() +
+![]() ∠A
∠A
![]()
(2)由题意得,∵∠BIC是△CEI的外角,
∴∠BIC=∠IEC+∠ICE(三角形外角定理),
∵∠IEC是△ABE的外角,
∴∠IDC=∠A+∠ABD(三角形外角定理),
∵BI、CI是∠ABC、∠ACB的平分线,
∴∠ABE=![]() ∠ABC,∠ICE=
∠ABC,∠ICE=![]() ∠ACB(角平分线定义),
∠ACB(角平分线定义),
∴∠BIC=![]() (∠ABC+∠ACB)+∠A=
(∠ABC+∠ACB)+∠A=![]() (
(![]() ∠A)+∠A=
∠A)+∠A=![]() +
+![]() ∠A
∠A
![]()
(3) 根据上述规律可得,∠BIC=90°+![]() ∠A.或∠A =2∠BIC - 180°
∠A.或∠A =2∠BIC - 180°
理由如下:
∵∠BIC是△CEI的外角,
∴∠BIC=∠IEC+∠ICE(三角形外角定理),
∵∠IEC是△ABE的外角,
∴∠IDC=∠A+∠ABD(三角形外角定理),
∵BI、CI是∠ABC、∠ACB的平分线,
∴∠ABE=![]() ∠ABC,∠ICE=
∠ABC,∠ICE=![]() ∠ACB(角平分线定义),
∠ACB(角平分线定义),
∴∠BIC=![]() (∠ABC+∠ACB)+∠A=
(∠ABC+∠ACB)+∠A=![]() (
(![]() ∠A)+∠A=
∠A)+∠A=![]() +
+![]() ∠A.
∠A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )

A. y=x+12 B. y=0.5x+12
C. y=0.5x+10 D. y=x+10.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N.
(1)观察图1,直接写出∠AEM与∠BNE的关系是;(不用证明)
(2)如图1,当M、N都分别在AB、BC上时,可探究出BN与AM的关系为:;(不用证明)
(3)如图2,当M、N都分别在AB、BC的延长线上时,(2)中BN与AM的关系式是否仍然成立?若成立,请说明理由:若不成立,写出你认为成立的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知分式![]() .
.
(1)当____时,分式的值等于零;
(2)当____时,分式无意义;
(3)当___且___时分式的值是正数;
(4)当____时,分式的值是负数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b经过点A(5,0),B(1,4).

(1)求直线AB的表达式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式kx+b>2x-4>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,点
,点![]() 是直线
是直线![]() 上一点(不与
上一点(不与![]() 重合),以
重合),以![]() 为一边在
为一边在![]() 的右侧作
的右侧作![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)如图1,当点![]() 在线段
在线段![]() 上,如果
上,如果![]() ,则
,则![]() 度;
度;
(2)设![]() ,
, ![]() .
.
①如图2,当点![]() 在线段
在线段![]() 上移动,则
上移动,则![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点![]() 在直线
在直线![]() 上移动,则
上移动,则![]() 之间有怎样的数量关系?请画出图形并直接写出相应的结论.
之间有怎样的数量关系?请画出图形并直接写出相应的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4>=5,<-1.5>=-1.
解决下列问题:
(1)[-4.5]=___,<3.5>=___;
(2)若[x]=2,则x的取值范围是___;若<y>=-1,则y的取值范围是___.
(3)已知x,y满足方程组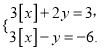 求x,y的取值范围.
求x,y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com