
分析 (1)根据观察,可得规律$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$;
(2)根据规律,可简便运算.
解答 解:(1)$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$;
故答案是:$\sqrt{n}$-$\sqrt{n-1}$;
(2)原式=($\sqrt{2}$-1)+($\sqrt{3}$-$\sqrt{2}$)+($\sqrt{4}$-$\sqrt{3}$)+($\sqrt{5}$-$\sqrt{4}$)+…+($\sqrt{2013}$-$\sqrt{2012}$)
=$\sqrt{2013}$-1.
点评 本题考查了分母有理化,利用了平方差公式进行分母有理化.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
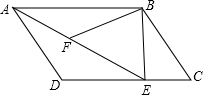 如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C,求证:△ABF∽△EAD.
如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE=∠C,求证:△ABF∽△EAD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 水位变化(米) | 0.12 | -0.02 | -0.13 | -0.20 | -0.08 | -0.02 | 0.32 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
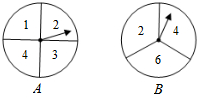 如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字,现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字,现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com