
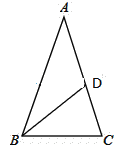
【题目】如图,△ABC中,∠A=36°,∠C=72°,∠DBC=36°.
(1)求∠ABD的度数。
(2)求证:BC=AD.
科目:初中数学 来源: 题型:
【题目】如图(1),A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以1.5m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示. 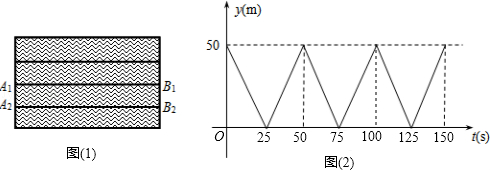
(1)赛道的长度是m,甲的速度是m/s;当t=s时,甲、乙两人第一次相遇,当t=s时,甲、乙两人第二次相遇?
(2)第三次相遇时,两人距池边B1B2多少米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= ![]() 在第一象限的图象经过点B,与OA交于点P,且OA2﹣AB2=18,则点P的横坐标为( )
在第一象限的图象经过点B,与OA交于点P,且OA2﹣AB2=18,则点P的横坐标为( ) 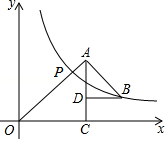
A.9
B.6
C.3
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段, ![]() ≈1.414,
≈1.414, ![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 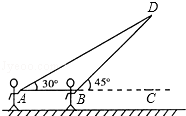
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E. 
(1)线段AE=;
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F. 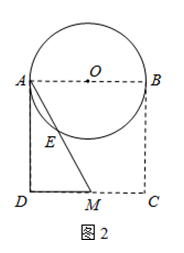
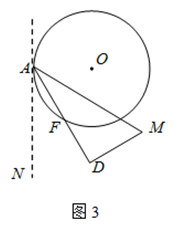
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α= ![]() 时,DM与⊙O相切.
时,DM与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副含 ![]() 和
和 ![]() 角的三角板
角的三角板 ![]() 和
和 ![]() 叠合在一起,边
叠合在一起,边 ![]() 与
与 ![]() 重合,
重合, ![]() (如图1),点
(如图1),点 ![]() 为边
为边 ![]()
![]() 的中点,边
的中点,边 ![]() 与
与 ![]() 相交于点
相交于点 ![]() .现将三角板
.现将三角板 ![]() 绕点
绕点 ![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 ![]() 从
从 ![]() 到
到 ![]() 的变化过程中,点
的变化过程中,点 ![]() 相应移动的路径长为 . (结果保留根号)
相应移动的路径长为 . (结果保留根号)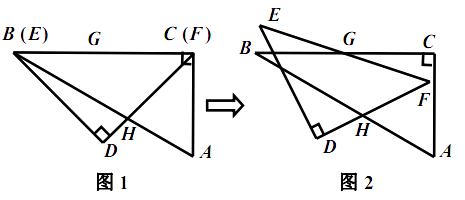
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1和∠2互为补角,∠A=∠D.求证:AB∥CD.
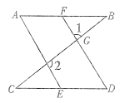
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(______).
又∠1和∠2互为补角(已知),
∴∠CGD和∠2互为补角,
∴AE∥FD(_________),
∴∠A=∠BFD(_______).
∵∠A=∠D(已知),
∴∠BFD=∠D(_______),
AB∥CD(______).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com