
����Ŀ���ŷ����Ǵ��ϲ����һ���˶��������������С�����������㳡�Ϸŷ��ݣ���ͼ������A����С���÷��ݹ�����һ�������ϣ����ݹ̶�����D������ʱ����AD��ˮƽ�ߵļн�Ϊ30�㣬Ϊ�˱��ڹ۲죬С��Ѹ����ǰ���ƶ������ߵ�������A��10��B������ʱ������BD��ˮƽ�ߵļн�Ϊ45�㣮��֪��A��B��C��ͬһ��ˮƽֱ���ϣ��������С����ʱ���ջصķ����ߵij����Ƕ����ף���������AD��BD��Ϊ�߶Σ� ![]() ��1.414��
��1.414�� ![]() ��1.732���������ȷ��1�ף���
��1.732���������ȷ��1�ף��� 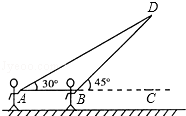
���𰸡��⣺��DH��BC��H����DH=x�ף� 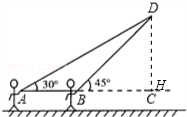
�ߡ�ACD=90�㣬
����ֱ�ǡ�ADH�У���DAH=30�㣬AD=2DH=2x��AH=DH��tan30��= ![]() x��
x��
��ֱ�ǡ�BDH�У���DBH=45�㣬BH=DH=x��BD= ![]() x��
x��
��AH��BH=AB=10�ף�
�� ![]() x��x=10��
x��x=10��
��x=5�� ![]() +1����
+1����
��С����ʱ���ջصķ��ݵij���Ϊ��
AD��BD=2x�� ![]() x=��2��
x=��2�� ![]() ����5��
����5�� ![]() +1���֣�2��1.414����5����1.732+1����8��
+1���֣�2��1.414����5����1.732+1����8��
����������DH��BC��H����DH=x�ף��������Ǻ�����ʾ��AH��BH�ij�������AH��BH=AB�õ�һ������x�ķ��̣��ⷽ�����x��ֵ���������AD��BD�ij������ɽ��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪��ABC�У�AB=6��AC=9��AD��BC��D��MΪAD����һ�㣬��MC2-MB2���ڣ��� ����

A. 9 B. 35 C. 45 D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����E��F�ֱ���������ABCD�ı�BC��CD�ϣ���EAF=45�㣬���ж�BE��EF��FD֮���������ϵ��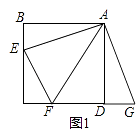
С�ϰѡ�ABE�Ƶ�A��ʱ����ת90������ADG��ͨ��֤����AEF�ա�AGF���Ӷ����ֲ�֤����EF=BE+FD��
��1����ͼ2����E��F�ֱ���������ABCD�ı�CB��CD���ӳ����ϣ���EAF=45�㣬����EF�������С�ϵķ��ָ������ʾд��EF��BE��DF֮���������ϵ����֤����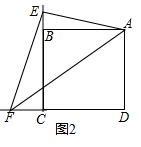
��2����ͼ3����ͼ����BAC=90�㣬AB=AC����E��F�ڱ�BC�ϣ��ҡ�EAF=45�㣬��BE=3��EF=5����CF�ij���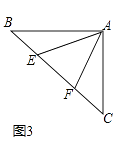
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֪ʶ��
�����dz�����ѧ��һ����Ҫ���ߣ�����������Խ�������������ϣ��о��������Ƿ�����������Ҫ�Ĺ���:
���磬��������![]() �㡢
�㡢![]() ���ʾ�����ֱ�Ϊ
���ʾ�����ֱ�Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ����֮��ľ���
����֮��ľ���![]() ���߶�
���߶�![]() ���е�
���е�![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ��
��
�������龳��
�������ϣ���![]() ��ʾ����Ϊ-20����
��ʾ����Ϊ-20����![]() ��ʾ����Ϊ10������
��ʾ����Ϊ10������![]() �ӵ�
�ӵ�![]() �����������������˶���ͬʱ������
�����������������˶���ͬʱ������![]() Ҳ�ӵ�
Ҳ�ӵ�![]() ���������Ḻ�����˶�����֪�˶���4����ʱ��
���������Ḻ�����˶�����֪�˶���4����ʱ��![]() ��
��![]() �����������Ҷ���
�����������Ҷ���![]() ��
��![]() �˶����ٶ�֮����
�˶����ٶ�֮����![]() ���ٶȵ�λ:��λ����/�룩��
���ٶȵ�λ:��λ����/�룩��
![]()
![]()
����ͼ
���ۺ����ã�
��1����![]() ���˶��ٶ�Ϊ______��λ����/�룬��
���˶��ٶ�Ϊ______��λ����/�룬��![]() ���˶��ٶ�Ϊ______��λ����/�룻
���˶��ٶ�Ϊ______��λ����/�룻
��2����![]() ʱ�����˶�ʱ�䣻
ʱ�����˶�ʱ�䣻
��3������![]() ��
��![]() �������������ԭ�����ٶ����������˶������˶��ķ����ޣ����Ƿ���:���Ŷ���
�������������ԭ�����ٶ����������˶������˶��ķ����ޣ����Ƿ���:���Ŷ���![]() ��
��![]() ���˶����߶�
���˶����߶�![]() ���е�
���е�![]() Ҳ�����˶����ʵ�
Ҳ�����˶����ʵ�![]() �ܷ���ԭ���غϣ����ܣ������
�ܷ���ԭ���غϣ����ܣ������![]() ��
��![]() ���������˶�ʱ�䣬��ֱ��д����
���������˶�ʱ�䣬��ֱ��д����![]() ���˶�������˶��ٶȣ������ܣ���˵�����ɣ�
���˶�������˶��ٶȣ������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ڵ�����ֱ�����ཻ��ƽ������λ�ù�ϵ��
��1����ͼ1����AB��CD����P��AB��CD�ڲ�����B=50������D=30��������BPD��
��2����ͼ2������P�Ƶ�AB��CD�ⲿ������BPD����B����D֮���к�������ϵ��������֤����
��3����ͼ3��д����BPD�p��B�p��D�p��BQD֮���������ϵ����֤����Ľ��ۣ�
��4����ͼ4�������A+��B+��C+��D+��E+��F�Ķ�����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=36�㣬��C=72�㣬��DBC=36��.
��1�����ABD�Ķ�����
��2����֤��BC=AD.
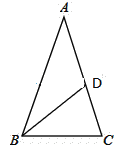
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ע����ͼ2��ȫ��ͬ�������κ���y= ![]() x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y�ύ�ڵ�C��
x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y�ύ�ڵ�C��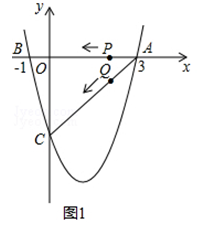
��1����ö��κ����Ľ���ʽ��
��2����������ߵĶ���ΪD�����ACD�����������ͼ1��̽������
��3������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶�����P��Q�˶���t��ʱ����APQ��PQ���ڵ�ֱ�߷��ۣ���Aǡ��������������E�㴦����ֱ���ж���ʱ�ı���APEQ����״�������E�����꣨����ͼ2��̽������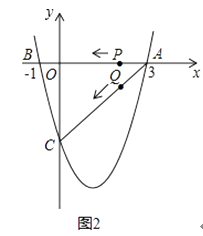
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��a��b�Ǹ�����������ijͬѧ�ֱ����x=-1,1,2,4ʱ����ʽax+b��ֵ�����εõ������ĸ��������֪����3������ȷ�ģ���ô������ǣ� ��
A. ![]() B. a+b=5 C. 2a+b=7 D. 4a+b=14
B. a+b=5 C. 2a+b=7 D. 4a+b=14
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=2��AO=BO��P��ֱ��CO�ϵ�һ�����㣬��AOC=60�㣬����PAB����BPΪֱ�DZߵ�ֱ��������ʱ��AP�ij�Ϊ�� ��
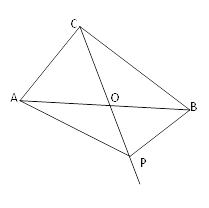
A. ![]() ,1,2 B.
,1,2 B. ![]() ,
,![]() ,2 C.
,2 C. ![]() ,
,![]() ,1 D.
,1 D. ![]() ��2
��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com