
ЁОЬтФПЁПЃЈБГОАжЊЪЖЃЉ
Ъ§жсЪЧГѕжаЪ§бЇЕФвЛИіживЊЙЄОпЃЌРћгУЪ§жсПЩвдНЋЪ§гыаЮЭъУРНсКЯЃЎбаОПЪ§жсЮвУЧЗЂЯжгааэЖрживЊЕФЙцТЩ:
Р§ШчЃЌШєЪ§жсЩЯ![]() ЕуЁЂ
ЕуЁЂ![]() ЕуБэЪОЕФЪ§ЗжБ№ЮЊ
ЕуБэЪОЕФЪ§ЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌдђ
ЃЌдђ![]() ЁЂ
ЁЂ![]() СНЕужЎМфЕФОрРы
СНЕужЎМфЕФОрРы![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЕФжаЕу
ЕФжаЕу![]() БэЪОЕФЪ§ЮЊ
БэЪОЕФЪ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈЮЪЬтЧщОГЃЉ
дкЪ§жсЩЯЃЌЕу![]() БэЪОЕФЪ§ЮЊ-20ЃЌЕу
БэЪОЕФЪ§ЮЊ-20ЃЌЕу![]() БэЪОЕФЪ§ЮЊ10ЃЌЖЏЕу
БэЪОЕФЪ§ЮЊ10ЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂбиЪ§жсе§ЗНЯђдЫЖЏЃЌЭЌЪБЃЌЖЏЕу
ГіЗЂбиЪ§жсе§ЗНЯђдЫЖЏЃЌЭЌЪБЃЌЖЏЕу![]() вВДгЕу
вВДгЕу![]() ГіЗЂбиЪ§жсИКЗНЯђдЫЖЏЃЌвбжЊдЫЖЏЕН4УыжгЪБЃЌ
ГіЗЂбиЪ§жсИКЗНЯђдЫЖЏЃЌвбжЊдЫЖЏЕН4УыжгЪБЃЌ![]() ЁЂ
ЁЂ![]() СНЕуЯргіЃЌЧвЖЏЕу
СНЕуЯргіЃЌЧвЖЏЕу![]() ЁЂ
ЁЂ![]() дЫЖЏЕФЫйЖШжЎБШЪЧ
дЫЖЏЕФЫйЖШжЎБШЪЧ![]() ЃЈЫйЖШЕЅЮЛ:ЕЅЮЛГЄЖШ/УыЃЉЃЎ
ЃЈЫйЖШЕЅЮЛ:ЕЅЮЛГЄЖШ/УыЃЉЃЎ
![]()
![]()
БИгУЭМ
ЃЈзлКЯдЫгУЃЉ
ЃЈ1ЃЉЕу![]() ЕФдЫЖЏЫйЖШЮЊ______ЕЅЮЛГЄЖШ/УыЃЌЕу
ЕФдЫЖЏЫйЖШЮЊ______ЕЅЮЛГЄЖШ/УыЃЌЕу![]() ЕФдЫЖЏЫйЖШЮЊ______ЕЅЮЛГЄЖШ/УыЃЛ
ЕФдЫЖЏЫйЖШЮЊ______ЕЅЮЛГЄЖШ/УыЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓдЫЖЏЪБМфЃЛ
ЪБЃЌЧѓдЫЖЏЪБМфЃЛ
ЃЈ3ЃЉШєЕу![]() ЁЂ
ЁЂ![]() дкЯргіКѓМЬајвддРДЕФЫйЖШдкЪ§жсЩЯдЫЖЏЃЌЕЋдЫЖЏЕФЗНЯђВЛЯоЃЌЮвУЧЗЂЯж:ЫцзХЖЏЕу
дкЯргіКѓМЬајвддРДЕФЫйЖШдкЪ§жсЩЯдЫЖЏЃЌЕЋдЫЖЏЕФЗНЯђВЛЯоЃЌЮвУЧЗЂЯж:ЫцзХЖЏЕу![]() ЁЂ
ЁЂ![]() ЕФдЫЖЏЃЌЯпЖЮ
ЕФдЫЖЏЃЌЯпЖЮ![]() ЕФжаЕу
ЕФжаЕу![]() вВЫцзХдЫЖЏЃЎЮЪЕу
вВЫцзХдЫЖЏЃЎЮЪЕу![]() ФмЗёгыдЕужиКЯЃПШєФмЃЌЧѓГіДг
ФмЗёгыдЕужиКЯЃПШєФмЃЌЧѓГіДг![]() ЁЂ
ЁЂ![]() ЯргіЦ№ОЙ§ЕФдЫЖЏЪБМфЃЌВЂжБНгаДГіЕу
ЯргіЦ№ОЙ§ЕФдЫЖЏЪБМфЃЌВЂжБНгаДГіЕу![]() ЕФдЫЖЏЗНЯђКЭдЫЖЏЫйЖШЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЕФдЫЖЏЗНЯђКЭдЫЖЏЫйЖШЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЖЏЕуPдЫЖЏЕФЫйЖШЮЊ4.5ЕЅЮЛГЄЖШ/УыЃЌЖЏЕуQдЫЖЏЕФЫйЖШЮЊ3ЕЅЮЛГЄЖШ/УыЃЛЃЈ2ЃЉдЫЖЏЪБМфЮЊ![]() Лђ
Лђ![]() УыЃЛЃЈ3ЃЉЕуMФмгыдЕужиКЯЃЌЫќбиЪ§жсе§ЗНЯђдЫЖЏЃЌдЫЖЏЫйЖШЮЊ
УыЃЛЃЈ3ЃЉЕуMФмгыдЕужиКЯЃЌЫќбиЪ§жсе§ЗНЯђдЫЖЏЃЌдЫЖЏЫйЖШЮЊ![]() ЛђбиЪ§жсе§ЗНЯђдЫЖЏЃЌдЫЖЏЫйЖШЮЊ
ЛђбиЪ§жсе§ЗНЯђдЫЖЏЃЌдЫЖЏЫйЖШЮЊ![]() ЃЌРэгЩМћНтЮі
ЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЩшЖЏЕуPдЫЖЏЕФЫйЖШЗжБ№ЮЊ3xЕЅЮЛГЄЖШ/УыЃЌQдЫЖЏЕФЫйЖШЗжБ№ЮЊ2xЕЅЮЛГЄЖШ/УыЃЎИљОнЁАдЫЖЏЕН4УыжгЪБЃЌPЁЂQСНЕуЯргіЁБСаЗНГЬЃЌЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЩшдЫЖЏЪБМфЮЊtУыЃЎЕуPБэЪОЕФЪ§ЮЊЃ20ЃЋ4.5tЃЌЕуQБэЪОЕФЪ§ЮЊ10Ѓ3tЃЌИљОнЁАPQ=![]() ABЁБЃЌСаЗНГЬЃЌЧѓНтМДПЩЃЛ
ABЁБЃЌСаЗНГЬЃЌЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЯШЧѓГіPЁЂQЯргіЕуБэЪОЕФЪ§ЃЌЩшДгPЁЂQЯргіЦ№ОЙ§ЕФдЫЖЏЪБМфЮЊtУыЪБЃЌPQЕФжаЕуMгыдЕужиКЯЃЌЧѓГіPЁЂQДЫЪББэЪОЕФЪ§ЃЎШЛКѓЗжЫФжжЧщПіСаЗНГЬЃЌЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЩшЖЏЕуPдЫЖЏЕФЫйЖШЗжБ№ЮЊ3xЕЅЮЛГЄЖШ/УыЃЌQдЫЖЏЕФЫйЖШЗжБ№ЮЊ2xЕЅЮЛГЄЖШ/УыЃЎИљОнЬтвтЕУЃК
4ЁС3xЃЋ4ЁС2x=30ЃЌЃЈЛђЃ20ЃЋ4ЁС3x=10Ѓ4ЁС2xЃЉ
НтЕУЃКx=1.5ЃЎ
3x=4.5ЃЈЕЅЮЛГЄЖШ/УыЃЉЃЌ2x=3ЃЈЕЅЮЛГЄЖШ/УыЃЉЃЎ
Д№ЃКЖЏЕуPдЫЖЏЕФЫйЖШЮЊ4.5ЕЅЮЛГЄЖШ/УыЃЌЖЏЕуQдЫЖЏЕФЫйЖШЮЊ3ЕЅЮЛГЄЖШ/УыЃЎ
ЃЈ2ЃЉЩшдЫЖЏЪБМфЮЊtУыЃЎ
гЩЬтвтжЊЃКЕуPБэЪОЕФЪ§ЮЊЃ20ЃЋ4.5tЃЌЕуQБэЪОЕФЪ§ЮЊ10Ѓ3tЃЌИљОнЬтвтЕУЃК
|ЃЈЃ20ЃЋ4.5tЃЉЃЃЈ10Ѓ3tЃЉ|=![]() ЁС|ЃЈЃ20ЃЉЃ10|
ЁС|ЃЈЃ20ЃЉЃ10|
ећРэЕУЃК|7.5tЃ30|=10
7ЃЎ5tЃ30=10Лђ7.5tЃ30=Ѓ10
НтЕУЃКt=![]() Лђt=
Лђt=![]() ЃЎ
ЃЎ
Д№ЃКдЫЖЏЪБМфЮЊ![]() Лђ
Лђ![]() УыЃЎ
УыЃЎ
ЃЈ3ЃЉPЁЂQЯргіЕуБэЪОЕФЪ§ЮЊЃ20ЃЋ4ЁС4.5=Ѓ2ЃЈзЂЃКЕБPЁЂQСНЕужиКЯЪБЃЌЯпЖЮPQЕФжаЕуMвВгыPЁЂQСНЕужиКЯЃЉ
ЩшДгPЁЂQЯргіЦ№ОЙ§ЕФдЫЖЏЪБМфЮЊtУыЪБЃЌЕуMгыдЕужиКЯЃЎ
ЂйЕуPЁЂQОљбиЪ§жсе§ЗНЯђдЫЖЏЃЌдђЃК
![]()
НтЕУЃКt=![]() ЃЎ
ЃЎ
ДЫЪБЕуMФмгыдЕужиКЯЃЌЫќбиЪ§жсе§ЗНЯђдЫЖЏЃЌдЫЖЏЫйЖШЮЊ2ЁТ![]() ЃЈЕЅЮЛГЄЖШ/УыЃЉЃЛ
ЃЈЕЅЮЛГЄЖШ/УыЃЉЃЛ
ЂкЕуPбиЪ§жсе§ЗНЯђдЫЖЏЃЌЕуQбиЪ§жсИКЗНЯђдЫЖЏЃЌдђЃК
![]()
НтЕУЃКt=![]() ЃЎ
ЃЎ
ДЫЪБЕуMФмгыдЕужиКЯЃЌЫќбиЪ§жсе§ЗНЯђдЫЖЏЃЌдЫЖЏЫйЖШЮЊ2ЁТ![]() =
=![]() ЃЈЕЅЮЛГЄЖШ/УыЃЉЃЛ
ЃЈЕЅЮЛГЄЖШ/УыЃЉЃЛ
ЂлЕуPбиЪ§жсИКЗНЯђдЫЖЏЃЌЕуQбиЪ§жсе§ЗНЯђдЫЖЏЃЌдђЃК
![]()
НтЕУЃКt=Ѓ![]() ЃЈЩсШЅЃЉЃЎ
ЃЈЩсШЅЃЉЃЎ
ДЫЪБЕуMВЛФмгыдЕужиКЯЃЛ
ЂмЕуPбиЪ§жсИКЗНЯђдЫЖЏЃЌЕуQбиЪ§жсИКЗНЯђдЫЖЏЃЌдђЃК
![]()
НтЕУЃКt=Ѓ![]() ЃЈЩсШЅЃЉЃЎ
ЃЈЩсШЅЃЉЃЎ
ДЫЪБЕуMВЛФмгыдЕужиКЯЃЎ
злЩЯЫљЪіЃКЕуMФмгыдЕужиКЯЃЌЫќбиЪ§жсе§ЗНЯђдЫЖЏЃЌдЫЖЏЫйЖШЮЊ![]() ЛђбиЪ§жсе§ЗНЯђдЫЖЏЃЌдЫЖЏЫйЖШЮЊ
ЛђбиЪ§жсе§ЗНЯђдЫЖЏЃЌдЫЖЏЫйЖШЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃРћгУЖўЮЌТыНјаабЇЩњбЇКХЭГвЛБрХХЃЎКкЩЋаЁе§ЗНаЮБэЪО1ЃЌАзЩЋаЁе§ЗНаЮБэЪО0ЃЌНЋУПвЛааЪ§зжДгзѓЕНгввРДЮМЧЮЊaЃЌbЃЌcЃЌdЃЌФЧУДРћгУЙЋЪН![]() МЦЫуГіУПвЛааЕФЪ§ОнЃЎЕквЛааБэЪОФъМЖЃЌЕкЖўааБэЪОАрМЖЃЌЕкШ§ааБэЪОАрМЖбЇКХЕФЪЎЮЛЪ§ЃЌЕкЫФааБэЪОАрМЖбЇКХЕФИіЮЛЪ§ЃЎШчЭМ1ЫљЪОЃЌЕквЛааЪ§зжДгзѓЭљгввРДЮЪЧ1ЃЌ0ЃЌ0ЃЌ1ЃЌдђБэЪОЕФЪ§ОнЮЊ1ЁС23+0ЁС22+0ЁС21+1=9ЃЌМЦзї09ЃЌЕкЖўааЪ§зжДгзѓЭљгввРДЮЪЧ1ЃЌ0ЃЌ1ЃЌ0ЃЌдђБэЪОЕФЪ§ОнЮЊ1ЁС23+0ЁС22+1ЁС21=10ЃЌМЦзї10ЃЌвдДЫРрЭЦЃЌЭМ1ДњБэЕФЭГвЛбЇКХЮЊ091034ЃЌБэЪО9ФъМЖ10Ар34КХЃЎаЁУїЫљЖдгІЕФЖўЮЌТыШчЭМ2ЫљЪОЃЌдђЫћЕФЭГвЛбЇКХЮЊ_______ЃЎ
МЦЫуГіУПвЛааЕФЪ§ОнЃЎЕквЛааБэЪОФъМЖЃЌЕкЖўааБэЪОАрМЖЃЌЕкШ§ааБэЪОАрМЖбЇКХЕФЪЎЮЛЪ§ЃЌЕкЫФааБэЪОАрМЖбЇКХЕФИіЮЛЪ§ЃЎШчЭМ1ЫљЪОЃЌЕквЛааЪ§зжДгзѓЭљгввРДЮЪЧ1ЃЌ0ЃЌ0ЃЌ1ЃЌдђБэЪОЕФЪ§ОнЮЊ1ЁС23+0ЁС22+0ЁС21+1=9ЃЌМЦзї09ЃЌЕкЖўааЪ§зжДгзѓЭљгввРДЮЪЧ1ЃЌ0ЃЌ1ЃЌ0ЃЌдђБэЪОЕФЪ§ОнЮЊ1ЁС23+0ЁС22+1ЁС21=10ЃЌМЦзї10ЃЌвдДЫРрЭЦЃЌЭМ1ДњБэЕФЭГвЛбЇКХЮЊ091034ЃЌБэЪО9ФъМЖ10Ар34КХЃЎаЁУїЫљЖдгІЕФЖўЮЌТыШчЭМ2ЫљЪОЃЌдђЫћЕФЭГвЛбЇКХЮЊ_______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯЬтЁЃ
ЃЈ1ЃЉМЦЫуЃКЃЈtan60ЁуЃЉЉ1ЁС ![]() Љ|Љ
Љ|Љ ![]() |+23ЁС0.125
|+23ЁС0.125
ЃЈ2ЃЉНтЗНГЬЃКЃЈxЉ5ЃЉ2=16ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЁїOACКЭЁїBADЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯACO=ЁЯADB=90ЁуЃЌЗДБШР§КЏЪ§y= ![]() дкЕквЛЯѓЯоЕФЭМЯѓОЙ§ЕуBЃЌгыOAНЛгкЕуPЃЌЧвOA2ЉAB2=18ЃЌдђЕуPЕФКсзјБъЮЊЃЈ ЃЉ
дкЕквЛЯѓЯоЕФЭМЯѓОЙ§ЕуBЃЌгыOAНЛгкЕуPЃЌЧвOA2ЉAB2=18ЃЌдђЕуPЕФКсзјБъЮЊЃЈ ЃЉ 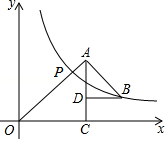
A.9
B.6
C.3
D.3 ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫожнЪаИпаТЧјФГЕчзгЕчТЗАхГЇЕНАВЛеДѓбЇДг2018ФъгІНьБЯвЕЩњжаеаЦИЙЋЫОжАдБЃЌЖдгІЦИепЕФзЈвЕжЊЪЖЁЂгЂгяЫЎЦНЁЂВЮМгЩчЛсЪЕМљгыЩчЭХЛюЖЏЕШШ§ЯюНјааВтЪдЛђГЩЙћШЯЖЈЃЌШ§ЯюЕФЕУЗжТњЗжЖМЮЊ100ЗжЃЌШ§ЯюЕФЗжЪ§ЗжБ№АД5ЁУ3ЁУ2ЕФБШР§МЧШыУПШЫЕФзюКѓзмЗжЃЌга4ЮЛгІЦИепЕФЕУЗжШчЯТБэЫљЪОЃЎ
| зЈвЕжЊЪЖ | гЂгяЫЎЦН | ВЮМгЩчЛсЪЕМљгы ЩчЭХЛюЖЏЕШ |
Мз | 85 | 85 | 90 |
вв | 85 | 85 | 70 |
Бћ | 80 | 90 | 70 |
ЖЁ | 90 | 90 | 50 |
ЃЈ1ЃЉЗжБ№ЫуГі4ЮЛгІЦИепЕФзмЗжЃЛ
ЃЈ2ЃЉБэжаЫФШЫЁАзЈвЕжЊЪЖЁБЕФЦНОљЗжЮЊ85ЗжЃЌЗНВюЮЊ12.5ЃЌЫФШЫЁАгЂгяЫЎЦНЁБЕФЦНОљЗжЮЊ87.5ЗжЃЌЗНВюЮЊ6.25ЃЌЧыФуЧѓГіЫФШЫЁАВЮМгЩчЛсЪЕМљгыЩчЭХЛюЖЏЕШЁБЕФЦНОљЗжМАЗНВюЃЛ
ЃЈ3ЃЉЗжЮіЃЈ1ЃЉКЭЃЈ2ЃЉжаЕФгаЙиЪ§ОнЃЌФуЖдДѓбЇЩњгІЦИепгаКЮНЈвщЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮжНЦЌABCDжаЃЌABЃН4ЃЌBCЃН6ЃЌНЋЁїABCбиACелЕўЃЌЪЙЕуBТфдкЕуEДІЃЌCEНЛADгкЕуFЃЌдђDFЕФГЄЕШгк(ЁЁЁЁ)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗХЗчѓнЪЧДѓМвЯВАЎЕФвЛжждЫЖЏЃЌаЧЦкЬьЕФЩЯЮчаЁУїдкЪаеўИЎЙуГЁЩЯЗХЗчѓнЃЎШчЭМЃЌЫћдкAДІВЛаЁаФШУЗчѓнЙвдкСЫвЛПУЪїЩвЩЯЃЌЗчѓнЙЬЖЈдкСЫDДІЃЌДЫЪБЗчѓнADгыЫЎЦНЯпЕФМаНЧЮЊ30ЁуЃЌЮЊСЫБугкЙлВьЃЌаЁУїбИЫйЯђЧАБпвЦЖЏЃЌЪеЯпЕНДяСЫРыAДІ10УзЕФBДІЃЌДЫЪБЗчѓнЯпBDгыЫЎЦНЯпЕФМаНЧЮЊ45ЁуЃЎвбжЊЕуAЃЌBЃЌCдкЭЌвЛЬѕЫЎЦНжБЯпЩЯЃЌЧыФуЧѓГіаЁУїДЫЪБЫљЪеЛиЕФЗчѓнЯпЕФГЄЖШЪЧЖрЩйУзЃПЃЈЗчѓнЯпADЃЌBDОљЮЊЯпЖЮЃЌ ![]() Ёж1.414ЃЌ
Ёж1.414ЃЌ ![]() Ёж1.732ЃЌзюКѓНсЙћОЋШЗЕН1УзЃЉЃЎ
Ёж1.732ЃЌзюКѓНсЙћОЋШЗЕН1УзЃЉЃЎ 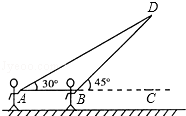
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпABЃЌCD ЯрНЛгкЕуOЃЌЁЯAOD=3ЁЯBOD+20Ёу.
(1)ЧѓЁЯBODЕФЖШЪ§ЃЛ
(2)вдOЮЊЖЫЕув§ЩфЯпOE,OF ,ЩфЯпOEЦНЗжЁЯBODЃЌЧвЁЯEOF= 90ЁуЃЌЧѓЁЯBOFЕФЖШЪ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкКсЯпЩЯЬюаДРэгЩЃЌЭъГЩЯТУцЕФжЄУїЃЎ ШчЭМЃЌвбжЊЁЯ1+ЁЯ2=180ЁуЃЌЁЯB=ЁЯ3ЃЌЧѓжЄЁЯC=ЁЯAED
жЄУїЃКЁпЁЯ1+ЁЯ2=180ЁуЃЈвбжЊЃЉЃЌЁЯ1+ЁЯDFE=180ЁуЃЈЃЉ
ЁрЁЯ2=ЁЯDFEЃЈЃЉ
ЁрABЁЮEFЃЈЃЉ
ЁрЁЯ3=ЁЯADEЃЈЃЉ
гжЁпЁЯB=ЁЯ3ЃЈвбжЊЃЉ
ЁрЁЯB=ЁЯADEЃЈЃЉ
ЁрDEЁЮBCЃЈЃЉ
ЁрЁЯC=ЁЯAEDЃЈЃЉ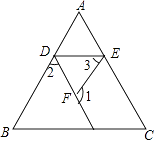
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com