
【题目】如图1(注:与图2完全相同),二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.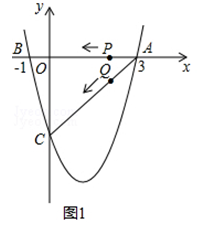
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).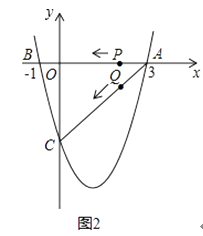
【答案】
(1)
解:∵二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
∴  ,
,
解得: 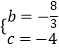 ,
,
∴y= ![]() x2﹣
x2﹣ ![]() x﹣4
x﹣4
(2)
解:过点D作DM⊥y轴于点M,

∵y= ![]() x2﹣
x2﹣ ![]() x﹣4=
x﹣4= ![]() (x﹣1)2﹣
(x﹣1)2﹣ ![]() ,
,
∴点D(1,﹣ ![]() )、点C(0,﹣4),
)、点C(0,﹣4),
则S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC
= ![]() ×(1+3)×
×(1+3)× ![]() ﹣
﹣ ![]() ×(
×( ![]() ﹣4)×1﹣
﹣4)×1﹣ ![]() ×3×4
×3×4
=4
(3)
解:四边形APEQ为菱形,E点坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).理由如下
).理由如下
如图2,E点关于PQ与A点对称,过点Q作,QF⊥AP于F,

∵AP=AQ=t,AP=EP,AQ=EQ
∴AP=AQ=QE=EP,
∴四边形AQEP为菱形,
∵FQ∥OC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]()
∴AF= ![]() t,FQ=
t,FQ= ![]() t
t
∴Q(3﹣ ![]() t,﹣
t,﹣ ![]() t),
t),
∵EQ=AP=t,
∴E(3﹣ ![]() t﹣t,﹣
t﹣t,﹣ ![]() t),
t),
∵E在二次函数y= ![]() x2﹣
x2﹣ ![]() x﹣4上,
x﹣4上,
∴﹣ ![]() t=
t= ![]() (3﹣
(3﹣ ![]() t)2﹣
t)2﹣ ![]() (3﹣
(3﹣ ![]() t)﹣4,
t)﹣4,
∴t= ![]() ,或t=0(与A重合,舍去),
,或t=0(与A重合,舍去),
∴E(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)将A,B点坐标代入函数y= ![]() x2+bx+c中,求得b、c,进而可求解析式;(2)由解析式先求得点D、C坐标,再根据S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC , 列式计算即可;(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、E对称,则AP=EP,AQ=EQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等的性质可用t表示E点坐标,又E在二次函数的图象上,所以代入即可求t,进而E可表示.
x2+bx+c中,求得b、c,进而可求解析式;(2)由解析式先求得点D、C坐标,再根据S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC , 列式计算即可;(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、E对称,则AP=EP,AQ=EQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等的性质可用t表示E点坐标,又E在二次函数的图象上,所以代入即可求t,进而E可表示.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点
A(0,4),点B是![]() 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宿州市高新区某电子电路板厂到安徽大学从2018年应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
| 专业知识 | 英语水平 | 参加社会实践与 社团活动等 |
甲 | 85 | 85 | 90 |
乙 | 85 | 85 | 70 |
丙 | 80 | 90 | 70 |
丁 | 90 | 90 | 50 |
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段, ![]() ≈1.414,
≈1.414, ![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 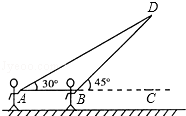
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4、P5、P6,…,则点P2018的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x=2,则2|x|-1=3.以上命题是真命题的有( ).
A. ①②③④ B. ①④ C. ②④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
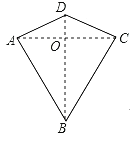
【题目】两组邻边相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中 AB=CB,AD=CD,詹姆斯在探究筝形的性质时,得到如下结论:① ACBD;②AOCO![]() AC;③△ABD≌△CBD;④四边形ABCD的面积=
AC;③△ABD≌△CBD;④四边形ABCD的面积=![]() ACBD,其中,正确的结论有_____.
ACBD,其中,正确的结论有_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com