
【题目】如图1,在边长为4的正△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB﹣BC运动,到点C停止.过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5.5秒时,PD的长是( )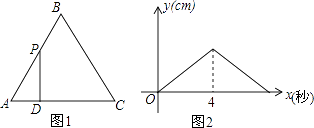
A.![]() cm
cm
B.![]() cm
cm
C.2 ![]() cm
cm
D.3 ![]() cm
cm
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
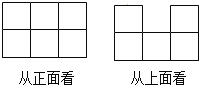
【题目】用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?
(1)它最多需要多少个小立方体?它最少需要多少个小立方体?
(2)请你画出这两种情况下的从左面看到的形状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
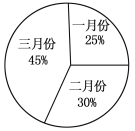
【题目】某服装专卖店老板对第一季度男、女服装销售收入进行统计,并绘制了扇形统计图.如图,由于三月份开展促销活动,男、女服装的销售收入分别比二月份增长了40%,64%,已知第一季度男女服装销售总收入为20万元.
(1)一月份销售收入为____万元,二月份销售收入为____万元,三月份的销售收入为____万元;
(2)二月份男、女服装的销售收入分别是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
线段的中点__________这条线段的“巧点”;(填“是”或“不是”).
若AB = 12cm,点C是线段AB的巧点,则AC=___________cm;
【解决问题】
(3) 如图②,已知AB=12cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动:点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s).当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数![]() 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则![]() 的值是( )
的值是( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B是数轴上的两个点,点A表示的数为13,点B表示的数为-5,动点P从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() 秒.
秒.
(1)BP= ,点P表示的数 (分别用含![]() 的代数式表示);
的代数式表示);
(2)点P运动多少秒时,PB=2PA?
(3)若M为BP的中点,N为PA的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) (湖南湘西24,10分)如图,已知矩形ABCD的两条对角线相交于O,∠ACB=30°,AB=2.
(1)求AC的长.
(2)求∠AOB的度数.
(3)以OB、OC为邻边作菱形OBEC,求菱形OBEC的面积.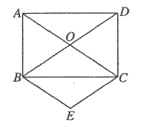
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 . 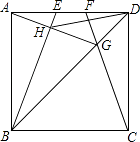
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个仓库共存有粮食60![]() .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:
(1)甲仓库运进粮食14![]() ,乙仓库运出粮食10
,乙仓库运出粮食10![]() 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
(2)如果甲仓库原有的粮食比乙仓库的2倍少3![]() ,则甲仓库运出多少
,则甲仓库运出多少![]() 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
(3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1![]() ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8![]() 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com