
����Ŀ��ij�������쳧������һ����ʽ�綯�������ƻ�һ��������װ240�������ڳ�������㹻���������������ʽ�綯�����İ�װ������������ƸһЩ�¹��ˣ����Ǿ�����ѵ���ϸڣ�Ҳ�ܶ������е綯�����İ�װ��������ʼ���в��ŷ��֣�1����������2���¹���ÿ�¿ɰ�װ8���綯������2����������3���¹���ÿ�¿ɰ�װ14���綯������
��1��ÿ�����������¹���ÿ�·ֱ����װ�������綯������
��2�����������Ƹn��0��n��10�����¹��ˣ�ʹ����Ƹ���¹��˺ͳ�����������պ������һ��İ�װ������ô�������ļ����¹��˵���Ƹ������
��3���ڣ�2���������£���������װ�綯������ÿ��������ÿ�·�2000Ԫ�Ĺ��ʣ���ÿ���¹���ÿ�·�1200Ԫ�Ĺ��ʣ���ô����Ӧ��Ƹ�������¹��ˣ�ʹ�¹��˵�����������������ͬʱ����ÿ��֧���Ĺ����ܶ�W��Ԫ�������ܵ��٣�
���𰸡�
��1���⣺��ÿ�����������¹���ÿ�·ֱ����װx��y���綯������
�������⣬�� ![]() ��
��
��� ![]() ��
��
��ÿ�����������¹���ÿ�·ֱ����װ4��2���綯����
��2���⣺�蹤����a����������
�������⣬��12��4a+2n��=240��
2a+n=10��
n=10��2a��
��a��n������������0��n��10��
����n=8��6��4��2��
��������4���¹��˵���Ƹ������
��n=8��a=1�����¹���8�ˣ�������1�ˣ�
��n=6��a=2�����¹���6�ˣ�������2�ˣ�
��n=4��a=3�����¹���4�ˣ�������3�ˣ�
��n=2��a=4�����¹���2�ˣ�������4��
��3���⣺��ϣ�2��֪��Ҫʹ�¹��˵�������������������n=8��a=1����n=6��a=2����n=4��a=3��
�������⣬��
W=2000a+1200n=2000a+1200��10��2a��=12000��400a��
Ҫʹ����ÿ��֧���Ĺ����ܶ�W��Ԫ�������ܵ��٣���aӦ���
��Ȼ��n=4��a=3ʱ������ÿ��֧���Ĺ����ܶ�W��Ԫ�������ܵ���
����������1����ÿ�����������¹���ÿ�·ֱ����װx��y���綯������
���ݡ�1����������2���¹���ÿ�¿ɰ�װ8���綯�������͡�2����������3���¹���ÿ�¿ɰ�װ14���綯�������з�������⣮��2���蹤����a���������������¹��˺ͳ�����������պ������һ��İ�װ������a��n������������0��n��10�����з���n��ֵ���������3������������ϵʽ������ʹ�¹��˵�����������������ͬʱ����ÿ��֧���Ĺ����ܶ�W��Ԫ�������ܵ��٣������������з�����
�����㾫�����������⣬������Ҫ�˽�һԪһ�β���ʽ���Ӧ��(1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д�������)��


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�����Ƴ�����ƽ��ÿ����۳�20����ÿ���� ӯ��40Ԫ��Ϊ������������������ӯ������ȡ�˽��۴�ʩ�������鷢�����ÿ���ƻ�����1Ԫ����ô�̳�ƽ��ÿ��ɶ��۳�2�������̳�ƽ��ÿ��ҪӮ��1200Ԫ����ÿ������Ӧ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����������ζ�Ӧ�ߵı�Ϊ3��10���������������ε��ܳ���Ϊ56cm�����С�������ε��ܳ�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С�顱�ľ�λͬѧΪ�����������ֱ�Ϊ20��10��15��15��18��17��12��14��11����λ��Ԫ������ô�������ݵ���λ���ǣ�������
A. 18 B. 15 C. 14 D. 17
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˽�ѧ���Ŀ������������ѧУ����Χ�ơ����������֡��������顢�����˶���������У�����ϲ���Ŀ�������������ʲô����ֻдһ�ࣩ�������⣬��ȫУ��Χ�������ȡ����ѧ�������ʾ����飬���������ʾ��ʵ���������Ƴ���ͼ��ʾ�IJ�����������ͳ��ͼ��������ϲ���������ֵ�ѧ��ռ����ȡ������12%���������������Ϣ����������⣺
��1������ε����У�һ����ȡ�˶�����ѧ����
��2����ϲ�����������ѧ��ռ����ȡ�����İٷ����Ƕ��٣�
��3�����ȫУ��1 000��ѧ�����������ȫУ��ϲ�������˶���ѧ��Լ�ж�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и���ʽ���У���ͬ������ǣ� ��
A.3x2y�멁3xy2
B.3xy�멁2yx
C.2x��2x2
D.5xy��5yz
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ȱߡ�ABC�߳�Ϊ6��AD�ǡ�ABC�����ߣ�PΪ�߶�AD���������˵�A��D����һ���㣬��CPΪһ������CP���·�����ͼ��ʾ�ĵȱߡ�CPE������BE�� 
��1����P���˶������У��߶�BE��APʼ�������˵˵������ɣ�
��2�����ӳ�BE��F��ʹ��CF=CE=5����ͼ2���ʣ� �������ʱAP�ij���
�ڵ���P���߶�AD���ӳ�����ʱ���ж�EF�ij��Ƿ�Ϊ��ֵ��������ֱ��д��EF�ij������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���D�������ǣ���3��1������A�������ǣ�4��3���� 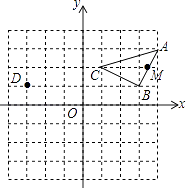
��1����B�͵�C������ֱ����� ��
��2������ABCƽ�ƺ�ʹ��C���D�غϣ���A��B���E��F�غϣ�������DEF��
��ֱ��д��E��F�����꣮
��3����AB�ϵĵ�M����Ϊ��x��y������ƽ�ƺ�Ķ�Ӧ��M�������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
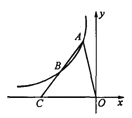
����Ŀ����ͼ��A��B�ǵڶ�������˫����y��![]() �ϵĵ㣬A��B����ĺ�����ֱ���a��2a���߶�AB���ӳ��߽�x���ڵ�C����S��AOC��6����k��ֵΪ ��
�ϵĵ㣬A��B����ĺ�����ֱ���a��2a���߶�AB���ӳ��߽�x���ڵ�C����S��AOC��6����k��ֵΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com