
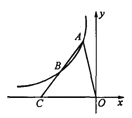
【题目】如图,A、B是第二象限内双曲线y=![]() 上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为 .
上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为 .
【答案】-4.
【解析】
试题分析:分别过点A、B作AF⊥y轴于点F,AD⊥x轴于点D,BG⊥y轴于点G,BE⊥x轴于点E,由于反比例函数的图象在第二象限,所以k<0,由点A是反比例函数图象上的点可知,S△AOD=S△AOF=![]() ,再由A、B两点的横坐标分别是a、2a可知AD=2BE,故点B是AC的二等分点,故DE=a,CE=a,所以S△AOC=S梯形ACOF-S△AOF=6,故可得出k的值.
,再由A、B两点的横坐标分别是a、2a可知AD=2BE,故点B是AC的二等分点,故DE=a,CE=a,所以S△AOC=S梯形ACOF-S△AOF=6,故可得出k的值.
试题解析:分别过点A、B作AF⊥y轴于点F,AD⊥x轴于点D,BG⊥y轴于点G,BE⊥x轴于点E,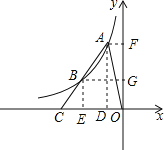
∵反比例函数y=![]() 的图象在第二象限,
的图象在第二象限,
∴k<0,
∵点A是反比例函数图象上的点,
∴S△AOD=S△AOF=![]() ,
,
∵A、B两点的横坐标分别是a、2a,
∴AD=2BE,
∴点B是AC的二等分点,
∴DE=a,CE=a,
∴S△AOC=S梯形ACOF-S△AOF=![]() (OE+CE+AF)×OF-
(OE+CE+AF)×OF-![]() =
=![]() ×4a×
×4a×![]() -
-![]() =6,
=6,
解得k=-4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能地少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点E为射线BC上一点,∠B+∠DCB=180°,连接ED,过点A的直线MN∥ED. 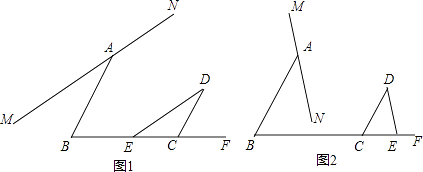
(1)如图1,当点E在线段BC上时,猜想并验证∠MAB=∠CDE.
(2)如图2,当点E在线段BC的延长线时,猜想并验证∠MAB与∠CDE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校在开展“三·五”奉献活动中,准备向镇敬老院捐赠一批帽子,已知买男式帽子用了180元,女式帽子的单价比男式帽子单价多2元.
(1)若原计划募捐380元,购买两种帽子共20顶,那么男、女式帽子的单价各是多少元?
(2)在这次捐款活动中,由于学生捐款踊跃,实际捐款566元,如果至少购买两种帽子共30顶,那么女式帽子最多能买几顶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一支原长为20cm的蜡烛,点燃后,其剩余长度y(cm)与燃烧时间x(min)之前的关系如表:
燃烧时间x(min) | 10 | 20 | 30 | 40 | 50 | … |
剩余长度y(cm) | 19 | 18 | 17 | 16 | 15 | … |
(1)表中反映的自变量是什么?因变量是什么?
(2)求出剩余长度y(cm)与燃烧时间x(min)之间的关系式;
(3)估计这支蜡烛最多可燃烧多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒. 
(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com