
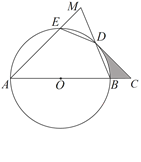
【题目】如图,AB是⊙O的直径,弧ED=弧BD,连接ED、BD,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)若OA![]() CD
CD![]()
![]() ,求阴影部分的面积;
,求阴影部分的面积;
(2)求证:DE![]() DM.
DM.
【答案】(1)4-π;(2)参见解析.
【解析】
试题(1)连接OD,由已知条件可证出三角形ODC是等腰直角三角形,OD的长度知道,∠DOB的度数是45度,这样,阴影的面积就等于等腰直角三角形ODC的面积减去扇形ODB的面积.(2)连接AD,由已知条件可证出AD垂直平分BM,从而得到DM=DB,又因为弧DE=弧DB,DE=DB,所以DE就等于DM了.
试题解析:(1)连接OD,∵CD是⊙O切线,∴OD⊥CD∵OA="CD" =![]() , OA=OD∴OD=CD=
, OA=OD∴OD=CD=![]() ∴△OCD 为等腰直角三角形∠DOC=∠C=45°S阴影=S△OCD-S扇OBD=
∴△OCD 为等腰直角三角形∠DOC=∠C=45°S阴影=S△OCD-S扇OBD=![]() ×
×![]() ×
×![]() -
-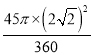
![]() .(2)连接AD.∵AB是⊙O直径∴∠ADB=∠ADM= 90°又∵弧ED=弧BD∴ED="BD" ∠MAD=∠BAD∴△AMD≌△ABD∴DM="BD" ∴DE=DM.如图所示:
.(2)连接AD.∵AB是⊙O直径∴∠ADB=∠ADM= 90°又∵弧ED=弧BD∴ED="BD" ∠MAD=∠BAD∴△AMD≌△ABD∴DM="BD" ∴DE=DM.如图所示:



科目:初中数学 来源: 题型:
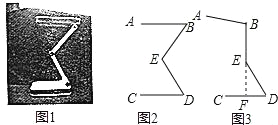
【题目】图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点B,E,D均为可转动点.现测得AB=BE=ED=CD=15cm,经多次调试发现当点B,E所在直线垂直经过CD的中点F时(如图3所示)放置较平稳.
(1)求平稳放置时灯座DC与灯杆DE的夹角的大小;
(2)为保护视力,写字时眼睛离桌面的距离应保持在30cm,为防止台灯刺眼,点A离桌面的距离应不超过30cm,求台灯平稳放置时∠ABE的最大值.(结果精确到0.01°,参考数据: ![]() ≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)
≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是![]()
![]()
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,
(1)求弦AC的长;
(2)求证:BC∥PA.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字6,-2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树状图的方法,求下列事件的概率:
(1)两次取出小球上的数字相同;
(2)两次取出小球上的数字之和大于10.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半?”(完成下列空格)
(1)当已知矩形A的边长分别为6和1时,小亮同学是这样研究的:
设所求矩形的两边分别是x和y,由题意得方程组: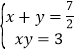 ,消去y化简得:2x2﹣7x+6=0,
,消去y化简得:2x2﹣7x+6=0,
∵△=49﹣48>0,
∴x1=_____,x2=_______,
∴满足要求的矩形B存在.
(2)如果已知矩形A的边长分别为2和1,请你仿照小亮的方法研究是否存在满足要求的矩形B.
(3)如果矩形A的边长为m和n,请你研究满足什么条件时,矩形B存在?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() .与
.与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上.
上.
(1)当![]() 随着
随着![]() 的增大而增大时,求自变量
的增大而增大时,求自变量![]() 的取值范围;
的取值范围;
(2)将抛物线![]() 向左平移
向左平移![]() 个单位,记平移后
个单位,记平移后![]() 随着
随着![]() 的增大而增大的部分为
的增大而增大的部分为![]() ,直线
,直线![]() 向下平移
向下平移![]() 个单位,当平移后的直线与
个单位,当平移后的直线与![]() 有公共点时,求
有公共点时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com