
����Ŀ��ij���й���һ��ţ�����ۣ��������ۣ�ʵ�ʼ۸�ÿǧ�˱�ԭ����2Ԫ������ԭ��������ţ��32ǧ�˵�Ǯ�����ڿ���33ǧ�ˣ�
��1������ʵ�ʹ�������ţ��ÿǧ�˶���Ԫ��
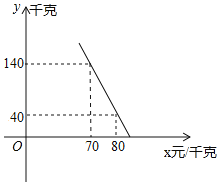
��2��������ţ���������y��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�������ͼ��ʾ��һ�κ�����ϵ����y��x֮��ĺ�����ϵʽ��
��3������ţ������۵��۶�Ϊ����ʱ���ܻ�����������������Ƕ��٣��������������멁������
���𰸡���1������ʵ�ʹ�������ţ��ÿǧ��64Ԫ����2����y����10x+840��������ţ������۵��۶�Ϊ74Ԫʱ���ܻ������������������1000Ԫ��
��������
��1��������ʵ�ʹ�������ţ��ÿǧ��xԪ������ԭ��������ţ��32ǧ�˵�Ǯ�����ڿ���33ǧ���г�����x��һԪһ�η��̣��ⷽ�̼��ɣ�
��2������y��x֮��ĺ�����ϵʽΪy=kx+b������70��1140������80��40�����룬���ô���ϵ�����������y��x֮��ĺ�����ϵʽ��
��������ţ������۵���ΪxԪʱ����������ΪwԪ����������=��������-�������õ�w����x�ĺ�����ϵʽΪw=-10��x-74��2+1000���ٸ��ݶ��κ��������ʼ�����⣮
��1��������ʵ�ʹ�������ţ��ÿǧ��aԪ����ԭ����������ţ��ÿǧ�ˣ�a+2��Ԫ�������⣬��
32��a+2����33a��
���a��64��
������ʵ�ʹ�������ţ��ÿǧ��64Ԫ��
��2������y��x֮��ĺ�����ϵʽΪy��kx+b��
����25��165������35��55�����룬
��![]() �����
�����![]() ��
��
��y��x֮��ĺ�����ϵʽΪy����10x+840��
��������ţ������۵���ΪxԪʱ����������ΪwԪ��
��w����x��64��y����x��64������10x+840������10x2+1480x��53760����10��x��74��2+1000��
���Ե�x��74ʱ��w�����ֵ1000��
�𣺽�����ţ������۵��۶�Ϊ74Ԫʱ���ܻ������������������1000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������Ӧ�������ĸﴴ�£��ܷ���Ϊ���ĺ��٣��ٰ����������ϵ�л����й�����ͼ��ı���ǵ伮��ͼ���۵�1.5�������˿���540Ԫ����ͼ�飬�ܵ������������ͼ�������ǡ�ñȵ�������伮��ͼ���������10����
��1�����е伮��ͼ��ı�ۣ�
��2���õ꾭��Ϊ���������߹��飬���Ϊ���������Ķ�������ͼ1��ʾ�ľ��¾��ΰ���ֽ����ͼ1�İ���ֽʾ��ͼ�У��������ۺۣ���Ӱ�Dzü����IJ��֣��ĽǾ�Ϊ��С��ͬ�������Σ������εı߳�Ϊ�۵���ȥ�Ŀ��ȣ���֪�ð���ֽ�����Ϊ875cm2������Ӱ���֣��������ÿ�����ͼ2�еġ��й����¡��Ȿ�飬����ij�Ϊ21cm����Ϊ15cm����Ϊ1cm����ֱ��д���ð���ֽ���Ȿ��ʱ�۵���ȥ�Ŀ��ȣ�
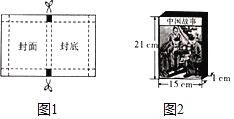
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
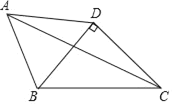
����Ŀ����ͼ�����ı���ABCD�У�AB��AD����BAD��60�㣬BC��4![]() �����Խ���BD��CD�ڵ�D����Խ���AC�����ֵ��
�����Խ���BD��CD�ڵ�D����Խ���AC�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
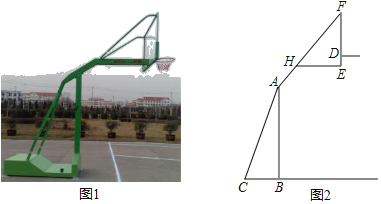
����Ŀ����ͼ1��2�ֱ���ij������ܵ�ʵ��ͼ��ʾ��ͼ��AB��BC�ڵ�B������BC��1.3�ף�����BC��֧��AC���ɵĽǡ�ACB��60������H��֧��AF�ϣ�����ײ�֧��EH��BC��EF��EH�ڵ�E����֪AH��![]() �ף�HF��
�ף�HF��![]() �ף�HE��1�ף�
�ף�HE��1�ף�
��1��������ײ�֧��HE��֧��AF���ɵġ�FHE�Ķ�����
��2��������ײ���E������ľ��룬����ȷ��0.01�ף����ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2��6ax+9a+1���߶�AB�н��㣬����֪��A��0��1�����B��2��3�������꣬��a��ȡֵ��Χ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣺��y��z��2+��x��y��2+��z��x��2=��y+z��2x��2+��z+x��2y��2+��x+y��2z��2��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ������������һ����Ϊ��һ������2������������ķ���Ϊ�����������������¹��ڱ������̵�˵������ȷ���ǣ� ��
������ʵ������������һ����Ϊ��һ������2������������ķ���Ϊ�����������������¹��ڱ������̵�˵������ȷ���ǣ� ��
�ٷ���![]() �DZ������̣�����
�DZ������̣�����![]() �DZ������̣���
�DZ������̣���![]() ��
��![]() ������
������![]() ��˫����
��˫����![]() ��ͼ���ϣ������
��ͼ���ϣ������![]() �ķ���
�ķ���![]() �DZ������̣�
�DZ������̣�
A. ��B. �٢�C. �٢�D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
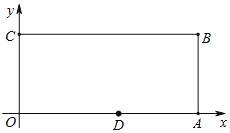
����Ŀ����ͼ����֪��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�dz����Σ���A��C��D������ֱ�ΪA(9��0)��C(0��4)��D(5��0)����P�ӵ�O��������ÿ��1����λ���ȵ��ٶ���O��C��B��A�˶�����P���˶�ʱ��Ϊt�룮��t��____��ʱ����ODP������Ϊ5�ĵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
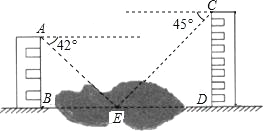
����Ŀ����ͼ������������AB��CD��AB��BD��CD��BD��AB=15m��CD=20m��AB��CD֮����һ���۳أ�С˫��A���ó�����Ȫ��E��ĸ���Ϊ42�㣬��C����E��ĸ���Ϊ45�㣬��B��E��D��ͬһֱ���ϣ�������������֮��ľ���BD���������ȷ��0.1m�����ο����ݣ�sin42��=0.67��cos42��=0.74��tan42��=0.90��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com