
【题目】如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.

(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得证;
(2)根据直角三角形两锐角互余得出∠CFA=90°-∠CAF,∠AED=90°-∠DAE,再根据角平分线的定义得出∠CAF=∠DAE,然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE.
试题解析:(1)∵∠ACB=90゜,CD⊥AB于D,
∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,
∴∠ACD=∠B;
(2)在Rt△AFC中,∠CFA=90°-∠CAF,
同理在Rt△AED中,∠AED=90°-∠DAE.
又∵AF平分∠CAB,
∴∠CAF=∠DAE,
∴∠AED=∠CFE,
又∵∠CEF=∠AED,
∴∠CEF=∠CFE.


科目:初中数学 来源: 题型:
【题目】第五次全国人口普查结果显示,我国的总人口已达到1300000000人,用科学记数法表示这个数,结果正确的是( )
A. 0.13×1010
B. 1.3×109
C. 13×108
D. 130×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”

小颖分别用24根和30根火柴棒摆出直角“整数三角形”
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.
(1)请你画出小颖和小辉摆出的“整数三角形”的示意图.
(2)你能否也从中取出若干根,摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.△ABC中,∠A=50°,求∠DBA+∠DCA的度数.
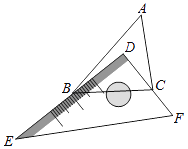
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】衢州新闻网2月16日讯,2013年春节“黄金周”全市接待游客总数为833100人次.将数833100用科学记数法表示应为( )
A.0.833×106
B.83.31×105
C.8.331×105
D.8.331×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为4,CD为⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC。

(1)求证:AB是⊙O的切线;
(2)求弦AC的长;
(3)求图中阴影部分的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答问题.
将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为x2-1,可设x4+x2-3=(x2-1)(x2+a)+b.
则x4+x2-3=(x2-1)(x2+a)+b=x4-x2+ax2-a+b=x4+(a-1)x2-a+b
∴![]() ,∴
,∴![]()
∴![]()
这样,分式![]() 被拆分成了一个整式x2+2与一个分式-
被拆分成了一个整式x2+2与一个分式-![]() 的和.
的和.
根据上述作法,将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式。
拆分成一个整式与一个分式(分子为整数)的和的形式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com