练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
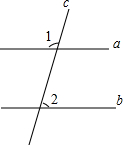
    5．如图，直线a，b被直线c所截，若直线a∥b，∠1=108°，则∠2的度数为（　　）
    A．108°B．82°C．72°D．62°

    分析 两直线平行，同位角相等．再根据邻补角的性质，即可求出∠2的度数．

    解答 解：∵a∥b，
    ∴∠1=∠3=108°，
    ∵∠2+∠3=180°，
    ∴∠2=72°，
    即∠2的度数等于72°．
    故选：C．

    点评 本题主要考查了平行线的性质以及邻补角，解题时注意：两直线平行，同位角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

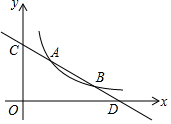    15．直线y=kx+b与反比例函数y=$\frac{6}{x}$（x＞0）的图象分别交于点 A（m，3）和点B（6，n），与坐标轴分别交于点C和点D．
    （1）求直线AB的解析式；
    （2）若点P是x轴上一动点，当△COD与△ADP相似时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列命题是假命题的是（　　）
    A．对顶角相等
    B．过直线外一点有且只有一条直线与已知直线平行
    C．两条直线被第三条直线所截，同旁内角互补
    D．在同一平面内，垂直于同一条直线的两条直线互相平行

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

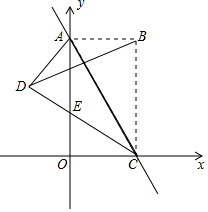    13．如图，在平面直角坐标系中，把矩形OABC沿对角线AC所在直线折叠，点B落在点D处，DC与y轴相交于点E，矩形OABC的边OC，OA的长是关于x的一元二次方程x2-12x+32=0的两个根，且OA＞OC．
    （1）求线段OA，OC的长；
    （2）求证：△ADE≌△COE，并求出线段OE的长；
    （3）直接写出点D的坐标；
    （4）若F是直线AC上一个动点，在坐标平面内是否存在点P，使以点E，C，P，F为顶点的四边形是菱形？若存在，请直接写出P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．乌江快铁大桥是快铁渝黔线的一项重要工程，由主桥AB和引桥BC两部分组成（如图所示），建造前工程师用以下方式做了测量：无人机在A处正上方97m处的P点，测得B处的俯角为30°（当时C处被小山体阻挡无法观测）．无人机飞行到B处正上方的D处时能看到C处，此时测得C处俯角为80°36′．
    （1）求主桥AB的长度；
    （2）若两观察点P、D的连线与水平方向的夹角为30°，求引桥BC的长．
    （长度均精确到1m，参考数据：$\sqrt{3}$≈1.73，sin80°36′≈0.987，cos80°36′≈0.163，tan80°36′≈6.06）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，在⊙O中，弦AB=8cm，OC⊥AB，垂足为C，OC=3cm，则⊙O的半径为5cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列四个数中，最大的数是（　　）
    A．3B．$\sqrt{3}$C．0D．π

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，在正方形网格中，每个小正方形的边长为1，则网格上的△ABC，其边长是无理数的有（　　）
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．将函数y=2x+3的图象位于x轴下方的部分沿x轴翻折至其上方后，所得的折线是函数y=|2x+3|的图象，若函数y=|2x+3|的图象在直线y=-$\frac{1}{4}$x+b下方的点的横坐标x满足-3＜x＜-1，则b的取值范围是-$\frac{9}{4}$＜b＜-$\frac{3}{4}$．

    查看答案和解析>>

    同步练习册答案