
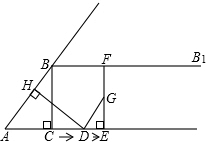
 ��ͼ����Rt��ABC�У���ACB=90�㣬AC=6��BC=8������B������BB1��AC������D�ӵ�A����������AC������ÿ��5����λ���ٶ��˶���ͬʱ����E�ӵ�C����������AC������ÿ��3����λ���ٶ��˶�������D��DH��AB��H������E��EF��AC������BB1��F������DF�����˶���ʱ��Ϊt�루t��0����
��ͼ����Rt��ABC�У���ACB=90�㣬AC=6��BC=8������B������BB1��AC������D�ӵ�A����������AC������ÿ��5����λ���ٶ��˶���ͬʱ����E�ӵ�C����������AC������ÿ��3����λ���ٶ��˶�������D��DH��AB��H������E��EF��AC������BB1��F������DF�����˶���ʱ��Ϊt�루t��0�������� ��1�������AB�������˶���ʾ��AD=5t������AD=AB�����������t���ɣ�
��2�����жϳ��ı���BCEF�Ǿ��Σ���AD��AE��AD��AE���������������ʽ���ɵó����ۣ�
��3�������жϳ���ABC�ס�ADH�ó�����ʽ���ɵó����ۣ�
���ҳ��ֽ�㣬����A'��������BB1�ϵĵ�Bʱ�����t=$\frac{5}{3}$������C'��������BB1��ʱ��t=$\frac{43}{15}$���ɵó����ۣ�
��� �⣺��1����Rt��ABC�У�AC=6��BC=8�����ݹ��ɶ����ã�AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10��
���˶�֪��AD=5t��
��AD=AB��
��5t=10��
��t=2��
��CD=AD-AC=10-6=4��CE=3t=6��
��DE=CE-CD=2��
�ʴ�Ϊ2��2��
��2���ߡ�ACB=90�㣬BB1��AC��EF��AC��
���ı���BCEF�Ǿ��Σ�EF=BC=8��
��AD��AEʱ��5t��6+3t��
��0��t��3��
��DE=AC����ACB�ա�DEF��DE=AE-AD=6+3t-5t=6-2t��
��6-2t=6��
��t=0��
��t��0���������⣬�ᣩ��
��AD��AEʱ��5t��6+3t��
��t��3��
��DE=AC����ACB�ա�DEF��DE=AD-AE=5t-6-3t=2t-6��
��2t-6=6��
��t=6��
�൱t=6ʱ����DEF���ACBȫ�ȣ�
��3������ͼ��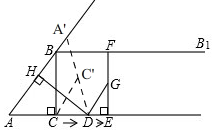
�ߡ�ACB=��AHD����BAC=��DAH��
���ABC�ס�ADH��
��$\frac{AB}{AD}=\frac{AC}{AH}=\frac{BC}{DH}$��
��$\frac{10}{5t}=\frac{6}{AH}=\frac{8}{DH}$��
��AH=3t��DH=4t��
��S��ADA'=2S��ADH=2��$\frac{1}{2}$AH��DH=AH��DH=12t2��
�ڵ���A'��������BB1�ϵĵ�Bʱ��AA'=AB=10��
��DH��AB��
��AA'=2AH=2��5t��cos��A=6t=10��
��t=$\frac{5}{3}$��
����C'��������BB1��ʱ��CC'��AB��
��BB1��AC��
���ı���ACC'BΪƽ���ı��Σ�
��CC'=AB=10��
��CC'=2CD��cos��A=2����5t-6����$\frac{6}{10}$=$\frac{6}{5}$��5t-6����
��t=$\frac{43}{15}$��
��$\frac{5}{3}$��t��$\frac{43}{15}$���߶�A'C'������BB1�й����㣮
���� �����Ǽ��α任�ۺ��⣬��Ҫ������ֱ�������ε����ʣ����ε��жϺ����ʣ�ȫ�������ε��жϺ����ʣ����������ε��ж������ʣ��⣨1���Ĺؼ�������AD=AB�������̣��⣨2���Ĺؼ��Ƿ�����������ۼ��㣬�⣨3���ٵĹؼ����жϳ���ABC�ס�ADH���⣨3���ڵĹؼ����ҳ��ֽ�㣬����ֽ��λ�õ�ʱ��t����һ���п������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
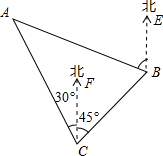 ��ͼ��A����C���ı�ƫ��30�㷽��B����C���ı�ƫ��45�㷽��A����B���ı�ƫ��70�㷽�����BAC�Ķ�����
��ͼ��A����C���ı�ƫ��30�㷽��B����C���ı�ƫ��45�㷽��A����B���ı�ƫ��70�㷽�����BAC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��ͼ1��һ���߳�Ϊa�������μ�ȥһ���߳�Ϊ1��С�����Σ�ͼ2��һ���߳�Ϊ��a-1���������Σ���ͼ1��ͼ2����Ӱ���ֵ�����ֱ�ΪS1��S2����$\frac{{S}_{1}}{{S}_{2}}$�ɻ���Ϊ$\frac{a+1}{a-1}$��
��ͼ��ʾ��ͼ1��һ���߳�Ϊa�������μ�ȥһ���߳�Ϊ1��С�����Σ�ͼ2��һ���߳�Ϊ��a-1���������Σ���ͼ1��ͼ2����Ӱ���ֵ�����ֱ�ΪS1��S2����$\frac{{S}_{1}}{{S}_{2}}$�ɻ���Ϊ$\frac{a+1}{a-1}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
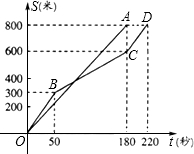 �ڽ������س���ѧҵˮƽ��������ѧ�Ƶ�Ů��800�����������У�ij����ͬʱ���ܵ�СӢ��С�����ܵ�·��S���ף�������ʱ��t���룩֮��ĺ���ͼ��ֱ�Ϊ�߶�OA������OBCD����ͼ������˵����ȷ���ǣ�������
�ڽ������س���ѧҵˮƽ��������ѧ�Ƶ�Ů��800�����������У�ij����ͬʱ���ܵ�СӢ��С�����ܵ�·��S���ף�������ʱ��t���룩֮��ĺ���ͼ��ֱ�Ϊ�߶�OA������OBCD����ͼ������˵����ȷ���ǣ�������| A�� | СӢ���ٶ���ʱ������������ | |
| B�� | С����ƽ���ٶȱ�СӢ��ƽ���ٶȴ� | |
| C�� | �����ܺ�180��ʱ���������� | |
| D�� | �����ܺ�50��ʱ��С����СӢ��ǰ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У�AB���д��߽�AB�ڵ㣬��BC�ڵ�D������ADC���ܳ�Ϊ17cm��AC=5cm����BC�ij�Ϊ��������
��ͼ���ڡ�ABC�У�AB���д��߽�AB�ڵ㣬��BC�ڵ�D������ADC���ܳ�Ϊ17cm��AC=5cm����BC�ij�Ϊ��������| A�� | 7cm | B�� | 10cm | C�� | 12cm | D�� | 22cm |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com