【题目】在20km越野赛中，甲乙两选手的行程y（单位：km）随时间x（单位：h）变化的图象
如图所示，根据图中提供的信息，有下列说法：
①两人相遇前，甲的速度小于乙的速度； ②出发后1小时，两人行程均为10km；
③出发后1.5小时，甲的行程比乙多3km； ④甲比乙先到达终点．
其中正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
浙江名校名师金卷系列答案科目：初中数学 来源： 题型：
【题目】我们给出如下定义：把对角线互相垂直的四边形叫做“对角线垂直四边形”.
如图，在四边形
中，
，四边形就是“对角线垂直四边形”.
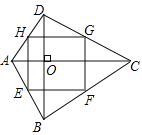
（1）下列四边形，一定是“对角线垂直四边形”的是_________.
①平行四边形 ②矩形 ③菱形 ④正方形
（2）如图，在“对角线垂直四边形”中，点
、
、
、
分别是边
、
、
、
的中点，求证：四边形
是矩形.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，△ABC是等腰直角三角形，
，
，四边形ADEF是正方形，点B、C分别在边AD、AF上，此时
，
成立．
（1）当△ABC绕点A逆时针旋转
时，如图②，成立吗？若成立，请证明；若不成立，请说明理由；
（2）当△ABC绕点A逆时针旋转45°时，如图③，延长DB交CF于点H；
（i）求证：；
（ii）当
，
时，则线段FC的长为_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”.如图1在
中，若
，则是“和谐三角形”.
（1）等边三角形一定是“和谐三角形”，是______命题（填“真”或“假”）.
（2）若
中，
，
，
，
，且
，若是“和谐三角形”，求
.
（3）如图2，在等边三角形
的边
，
上各取一点
，
，且
，
，
相交于点
，
是
的高，若
是“和谐三角形”，且
.
①求证：
.
②连结
，若
，那么线段
，
，
能否组成一个“和谐三角形”？若能，请给出证明：若不能，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，△ABC 的一边 AB 在 x 轴上，∠ABC=90°，点 C（4，8） 在第一象限内，AC 与 y 轴交于点 E，抛物线 y=
+bx+c 经过 A、B 两点，与 y 轴交于点 D（0，﹣6）．
（1）请直接写出抛物线的表达式；
（2）求 ED 的长；
（3）若点 M 是 x 轴上一点（不与点 A 重合），抛物线上是否存在点 N，使∠CAN=∠MAN．若存在，请直接写出点 N 的坐标；若不存在，请说明理由．
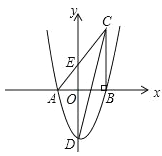
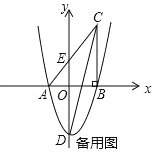
查看答案和解析>>
科目：初中数学 来源： 题型：
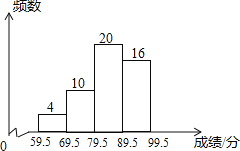
【题目】为增强学生环保意识，某中学组织全校3000名学生参加环保知识大赛，比赛成绩均为整数．从中抽取部分同学的成绩进行统计，并绘制成如下统计图．
请根据图中提供的信息，解答下列问题：
（1）若抽取的成绩用扇形图来描述，则表示“第二组（69.5~79.5）”的扇形的圆心角 度；
（2）若成绩在90分以上（含90分）的同学可获奖，请估计该校约有多少名同学获奖？
（3）某班准备从成绩最好的4名同学（男、女各2名）中随机选取2名同学去社区进行环保宣传，则选出的同学恰好是1男1女的概率为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC与△DCE有公共顶点C，AB=CD，BC=CE，∠ABC=∠DCE=90°.
（1）如图1，当点D在BC延长线上时.
①求证：△ABC≌△DCE.
②判断AC与DE的位置关系，并说明理由.
（2）如图2，△CDE从（1）中位置开始绕点C顺时针旋转，当点D落在BC边上时停止.
①若∠A=60°，记旋转的度数为
，当为何值时，DE与△ABC一边平行.
②如图3，若AB=c， BC=a， AC=b， a>c，边BC，DE交于点F，求整个运动过程中，F在BC上的运动路程（用含a， b， c的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下图是北京怀柔医院一位病人在4月8日6时到4月10日18时的体温记录示意图，下列说法中，错误的是
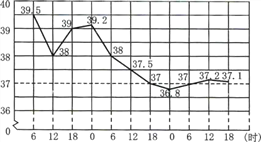
①护士每隔6小时给病人量一次体温；
②这个病人的体温最高是39.5摄氏度，最低36.8摄氏度；
③他的体温在4月9日18时到4月10日18时比较稳定；
④他的体温在4月8日18时到4月9日18时下降最快.
A. ① B. ②④ C. ④ D. ③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在锐角△ABC中，∠ABC=45°，高线AD、BE相交于点F．
（1）判断BF与AC的数量关系并说明理由；
（2）如图2，将△ACD沿线段AD对折，点C落在BD上的点M，AM与BE相交于点N，当DE∥AM时，判断NE与AC的数量关系并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
