
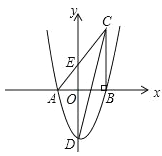
【题目】如图,在平面直角坐标系中,△ABC 的一边 AB 在 x 轴上,∠ABC=90°,点 C(4,8) 在第一象限内,AC 与 y 轴交于点 E,抛物线 y=![]() +bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
+bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
(1)请直接写出抛物线的表达式;
(2)求 ED 的长;
(3)若点 M 是 x 轴上一点(不与点 A 重合),抛物线上是否存在点 N,使∠CAN=∠MAN.若存在,请直接写出点 N 的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x﹣6;(2)
x﹣6;(2)![]() ;(3) S=﹣
;(3) S=﹣![]() m2+
m2+![]() m+26(﹣2<m<4);(4)满足条件的N点坐标为(
m+26(﹣2<m<4);(4)满足条件的N点坐标为(![]() ,
,![]() );(
);(![]() ,﹣
,﹣![]() ).
).
【解析】(1)先确定B(4,0),再利用待定系数法求出抛物线解析式为y=![]() x2-
x2-![]() x-6;
x-6;
(2)先利用待定系数法求得直线AC的解析式为y=![]() x+
x+![]() ,则可确定E(0,
,则可确定E(0,![]() ),然后计算DE的长;
),然后计算DE的长;
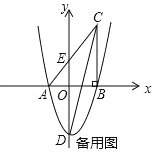
(3)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,根据角平分线的性质得FH=FB,易得AH=AB=6,再利用∠ACB的余弦可求出CF=5,则F(4,3),接着求出直线AF的解析式为y=![]() x+1,于是通过解方程组
x+1,于是通过解方程组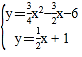 ,得N点坐标为(
,得N点坐标为(![]() ,
,![]() );当点M′在x的负半轴上时,AN′交y轴与G,先在证明∴Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组
);当点M′在x的负半轴上时,AN′交y轴与G,先在证明∴Rt△OAG∽Rt△BFA,在利用相似比求出OG=4,所以G(0,-4),接下来利用待定系数法求出直线AG的解析式为y=-2x-4,然后解方程组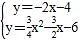 得N′的坐标.
得N′的坐标.
(1)∵BC⊥x轴,点C(4,8),
∴B(4,0),
把B(4,0),C(0,﹣6)代入y=![]() +bx+c得
+bx+c得![]() ,解得
,解得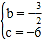 ,
,
∴抛物线解析式为y=![]() x﹣6;
x﹣6;
(2)设直线AC的解析式为y=px+q,
把A(﹣2,0),C(4,8)代入得![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为y=![]() x+
x+![]() ,
,
当x=0时,y=![]() x+
x+![]() =
=![]() ,则E(0,
,则E(0,![]() ),
),
∴DE=![]() +6=
+6=![]() ;
;
(3)如图2,当点M在x的正半轴,AN交BC于F,作FH⊥AC于H,
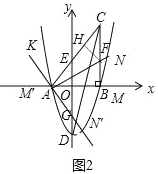
则FH=FB,
易得AH=AB=6,
∵AC=![]() ,
,
∴CH=10﹣6=4,
∵cos∠ACB=![]() ,
,
∴CF=![]() ,
,
∴F(4,3),
易得直线AF的解析式为y=![]() x+1,
x+1,
解方程组 得
得![]() 或
或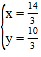 ,
,
∴N点坐标为(![]() ,
,![]() );
);
当点M′在x的负半轴上时,AN′交y轴与G,
∵∠CAN′=∠M′AN′,
∴∠KAM′=∠CAK,
而∠CAN=∠MAN,
∴∠KAC+∠CAN=90°,
而∠MAN+∠AFB=90°,
∴∠KAC=∠AFB,
而∠KAM′=∠GAO,
∴∠GAO=∠AFB,
∴Rt△OAG∽Rt△BFA,
∴![]() ,即
,即![]() ,解得OG=4,
,解得OG=4,
∴G(0,﹣4),
易得直线AG的解析式为y=﹣2x﹣4,
解方程组 得
得![]() 或
或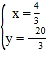 ,
,
∴N′的坐标为(![]() ,﹣
,﹣![]() ),
),
综上所述,满足条件的N点坐标为(![]() ,
,![]() );(
);(![]() ,﹣
,﹣![]() ).
).


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】王老师购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
①写出用含x、y的整式表示的地面总面积;
②若x=4m,y=1.5m,铺1m2地砖的平均费用为80元,求铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,![]() ,
,![]() ,
,![]() ,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
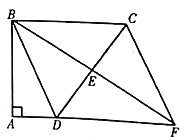
(1)求证:四边形BDFC是平行四边形;
(2)若![]() ,求四边形ABCF的周长.
,求四边形ABCF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点表示的数为
的中点表示的数为![]() .
.
(问题情境)
如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为![]() 秒(
秒(![]() ).
).
(综合运用)
(1)填空:
①![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ________,线段
________,线段![]() 的中点表示的数为__________.
的中点表示的数为__________.
②用含![]() 的代数式表示:
的代数式表示:![]() 秒后,点
秒后,点![]() 表示的数为____________;点
表示的数为____________;点![]() 表示的数为___________.
表示的数为___________.
③当![]() _________时,
_________时,![]() 、
、![]() 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.
(2)当![]() 为何值时,
为何值时,![]() .
.
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是边
是边![]() 上一动点,连结
上一动点,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() .小梦根据学习函数的经验,对
.小梦根据学习函数的经验,对![]() 的面积与
的面积与![]() 的长度之间的关系进行了探究:
的长度之间的关系进行了探究:

(1)设![]() 的长度为
的长度为![]() ,
,![]() 的面积
的面积![]() ,通过取
,通过取![]() 边上的不同位置的点
边上的不同位置的点![]() ,经分析和计算,得到了
,经分析和计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 |
| 1 | 0 |
| 2 | 3 |
根据上表可知,![]() ______,
______,![]() ______.
______.
(2)在平面直角坐标系![]() 中,画出(1)中所确定的函数的图象.
中,画出(1)中所确定的函数的图象.

(3)在(1)的条件下,令![]() 的面积为
的面积为![]() .
.
①用![]() 的代数式表示
的代数式表示![]() .
.
②结合函数图象.解决问题:当![]() 时,
时,![]() 的取值范围为______.
的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象
如图所示,根据图中提供的信息,有下列说法:
①两人相遇前,甲的速度小于乙的速度; ②出发后1小时,两人行程均为10km;
③出发后1.5小时,甲的行程比乙多3km; ④甲比乙先到达终点.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗。某食品厂为了了解市民对去年销量较好的肉馅(A)、豆沙馅(B)、菜馅(C)、三丁馅(D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整)。请根据以上信息回答:
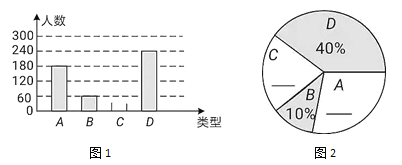
(1)从全体学生的调查表中随机抽取了多少名学生?
(2)将图1和图2补充完整;
(3)图2中表示“A”的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且![]() .
.
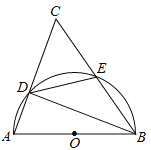
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是线段
是线段![]() 上一点,
上一点,![]() ,
,![]() 、
、![]() 两点分别从
两点分别从![]() 、
、![]() 出发以
出发以![]() 、
、![]() 的速度沿直线
的速度沿直线![]() 向左运动(
向左运动(![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 上),运动的时间为
上),运动的时间为![]() .
.

(1)当![]() 时,
时,![]() ,请求出
,请求出![]() 的长;
的长;
(2)当![]() 时,
时,![]() ,请求出
,请求出![]() 的长;
的长;
(3)若![]() 、
、![]() 运动到任一时刻时,总有
运动到任一时刻时,总有![]() ,请求出
,请求出![]() 的长;
的长;
(4)在(3)的条件下,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com