
【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且![]() .
.
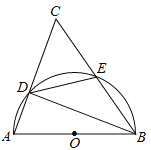
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求![]() 的值.
的值.
【答案】(1)等腰三角形;(2)![]()
【解析】
试题分析:根据AB是直径,则我们很容易知道![]() ,同时也是
,同时也是![]() .进而就有
.进而就有
![]() ,而又
,而又![]() ,则DE=BE,进而
,则DE=BE,进而![]() ,所以
,所以![]() ,而ABED可以看成是个圆内接四边形,则
,而ABED可以看成是个圆内接四边形,则![]() ,所以
,所以![]() ,即⊿ABC为等腰三角形.
,即⊿ABC为等腰三角形.
第(2)问要求的是![]() 的正弦值,由图知,
的正弦值,由图知,![]() 在
在![]() 中,AB=10,要求正弦值,就必须求得AD的值,在
中,AB=10,要求正弦值,就必须求得AD的值,在![]() 中,我们可以利用等腰三角形一腰上的高求出AD=2.8,这样我们就能求出
中,我们可以利用等腰三角形一腰上的高求出AD=2.8,这样我们就能求出![]() .
.
试题解析:(1)∵AB为直径,
∴∠ADC=∠BDE=90°,∠C+∠DBC=90°,∠CDE+∠EDB=90°,
又∵![]() ,
,
∴∠EDB=∠DBC,
∴∠C=∠CDE,
∴CE=DE,
∵![]() ,
,
∴DE=BE,CE=BE,
∴AE垂直平分BC,
∴AC=BC,
∴△ABC为等腰三角形.
∵A,B,E,D四点共圆,
∴∠CDE=∠CBA,∠C公用,
∴△CDE∽△CBA,
∴![]()
∵BC=12,半径为5,
由(1)得AC=BC=10,CE=6,
即![]()
解得CD=7.2,
∴AD=AC-CD=2.8;
∴sin∠ABD=![]() =
=![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1.5小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t=![]() 或t=
或t=![]() ,其中正确的结论有( )
,其中正确的结论有( )
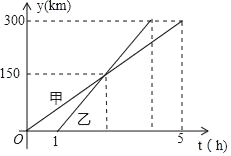
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
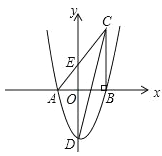
【题目】如图,在平面直角坐标系中,△ABC 的一边 AB 在 x 轴上,∠ABC=90°,点 C(4,8) 在第一象限内,AC 与 y 轴交于点 E,抛物线 y=![]() +bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
+bx+c 经过 A、B 两点,与 y 轴交于点 D(0,﹣6).
(1)请直接写出抛物线的表达式;
(2)求 ED 的长;
(3)若点 M 是 x 轴上一点(不与点 A 重合),抛物线上是否存在点 N,使∠CAN=∠MAN.若存在,请直接写出点 N 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△DCE有公共顶点C,AB=CD,BC=CE,∠ABC=∠DCE=90°.
(1)如图1,当点D在BC延长线上时.
①求证:△ABC≌△DCE.
②判断AC与DE的位置关系,并说明理由.
(2)如图2,△CDE从(1)中位置开始绕点C顺时针旋转,当点D落在BC边上时停止.
①若∠A=60°,记旋转的度数为![]() ,当
,当![]() 为何值时,DE与△ABC一边平行.
为何值时,DE与△ABC一边平行.
②如图3,若AB=c, BC=a, AC=b, a>c,边BC,DE交于点F,求整个运动过程中,F在BC上的运动路程(用含a, b, c的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票(“![]() 次”表示动车,“
次”表示动车,“![]() 次”表示高铁):
次”表示高铁):
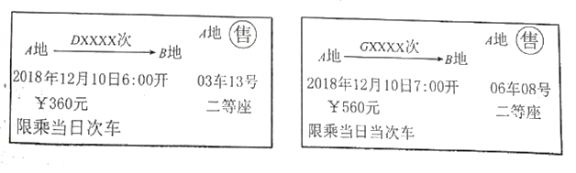
![]() 根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
根据车票中的信息填空:该列动车和高铁是 向而行(填“相”或“同”).
![]() 已知该动车和高铁的平均速度分别为
已知该动车和高铁的平均速度分别为![]() ,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2
,两列火车的长度不计.经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到2![]() .求
.求![]() 两地之间的距离.
两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是北京怀柔医院一位病人在4月8日6时到4月10日18时的体温记录示意图,下列说法中,错误的是
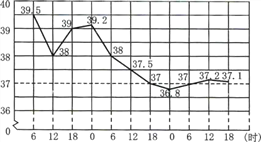
①护士每隔6小时给病人量一次体温;
②这个病人的体温最高是39.5摄氏度,最低36.8摄氏度;
③他的体温在4月9日18时到4月10日18时比较稳定;
④他的体温在4月8日18时到4月9日18时下降最快.
A. ① B. ②④ C. ④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 为其内部一条射线.
为其内部一条射线.
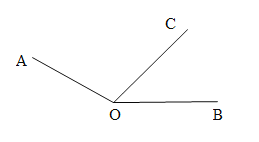
(1)若![]() 平分
平分![]() ,
,![]() 平分
平分![]() .求
.求![]() 的度数;
的度数;
(2)若![]() ,射线
,射线![]() 从
从![]() 起绕着
起绕着![]() 点顺时针旋转,旋转的速度是
点顺时针旋转,旋转的速度是![]() 每秒钟,设旋转的时间为
每秒钟,设旋转的时间为![]() ,试求当
,试求当![]()
![]()
![]()
![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照下列要求完成画图及相应的问题解答
(1)画直线![]() ;
;
(2)画![]() ;
;
(3)画线段![]() ;
;
(4)过![]() 点画直线
点画直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() ;
;
(5)请测量点![]() 到直线
到直线![]() 的距离为__________
的距离为__________![]() (精确到0.1
(精确到0.1 ![]() ) .
) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com