
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点表示的数为
的中点表示的数为![]() .
.
(问题情境)
如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为![]() 秒(
秒(![]() ).
).
(综合运用)
(1)填空:
①![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ________,线段
________,线段![]() 的中点表示的数为__________.
的中点表示的数为__________.
②用含![]() 的代数式表示:
的代数式表示:![]() 秒后,点
秒后,点![]() 表示的数为____________;点
表示的数为____________;点![]() 表示的数为___________.
表示的数为___________.
③当![]() _________时,
_________时,![]() 、
、![]() 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.
(2)当![]() 为何值时,
为何值时,![]() .
.
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长.
的长.

【答案】(1)①10;3;②![]() ;
;![]() ;③2;4;(2)当
;③2;4;(2)当![]() 或3时,
或3时,![]() ;(3)线段
;(3)线段![]() 的长度不变,是5.
的长度不变,是5.
【解析】
(1)根据题意即可得到结论;(2)由t秒后,点P表示的数-2+3t,点Q表示的数为8-2t,于是得到![]() ,列方程即可得到结论;(3)由点M表示的数为
,列方程即可得到结论;(3)由点M表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,即可得到线段
,即可得到线段![]() 的长,线段
的长,线段![]() =5,即线段
=5,即线段![]() 的长度不变;
的长度不变;
解:
(1)①∵![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,
表示的数为8,
∴![]() ,AB的中点表示为
,AB的中点表示为![]() ;
;
故答案为:10,3;
②∵数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,
∴点![]() 表示的数为
表示的数为![]() ;
;
∵点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,
出发,以每秒2个单位长度的速度向左匀速运动,
∴点![]() 表示的数为
表示的数为![]() ;
;
故答案为:![]() ;
;![]() ;
;
③依题意得,![]() =
=![]() ,
,
∴t=2,
此时P、Q两点相遇,相遇点所表示的数为:-2+6=4;
故答案为:2,4;
(2)∵![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() ,
,
答:当![]() 或3时,
或3时,![]() ,
,
(3)点![]() 表示的数为
表示的数为![]() ,
,
点![]() 表示的数为
表示的数为![]() ,
,
∴![]() ,
,
∴线段![]() 的长度不变,是5.
的长度不变,是5.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】已知树枝AB长为1.将树枝AB按照如下规则进行分形.其中1级分形图中,由B点处生长出两条树枝BD,BE,每条树枝长均为AB长的一半;在2级分形图中,D、E两点处生长出的每条树枝都等于DB长的一半.按照上面分形方法得到3级、4级分形图形.
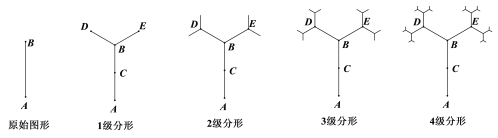
按照上面的规律,在3级分形图中,树枝长度的总和是_____________;
在n级分形图中,树枝总条数是___________(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
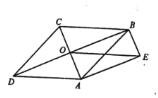
【题目】如图,平行四边形ABCD的对角线AC, BD相交于点O,且AE∥BD, BE∥AC, OE= CD.
(1)求证:四边形ABCD是菱形;
(2)若AD=2,则当四边形ABCD的形状是__________时,四边形AOBE的面积取得最大值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
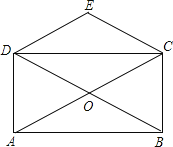
【题目】如图,矩形ABCD的对角线AC、BD交于点O,CE∥BD,DE∥AC.
(1)证明:四边形OCED为菱形;
(2)若AC=4,求四边形CODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.
(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD的长;若不能,请说明理由;
(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作ADEF.
①ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.
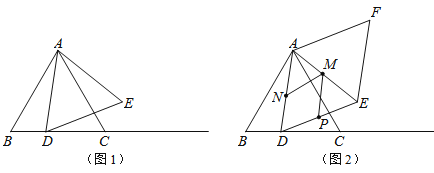
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
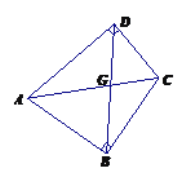
(1)如图,损矩形![]() 中,
中,![]() ,则该损矩形的直径是线段______.
,则该损矩形的直径是线段______.
(2)探究:在上述损矩形![]() 内,是否存在点
内,是否存在点![]() ,使
,使![]() 四个点都在以
四个点都在以![]() 为圆心的同一圆上,若存在,请指出点
为圆心的同一圆上,若存在,请指出点![]() 的具体位置___________________________;若不存在,请说明理由.
的具体位置___________________________;若不存在,请说明理由.
(3)实践:已知如图三条线段![]() ,求作相邻三边长顺次为
,求作相邻三边长顺次为![]() 的损矩形
的损矩形![]() (尺规作图,保留作图痕迹).
(尺规作图,保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.
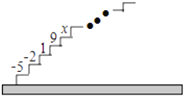
(尝试)(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数![]() 是多少?
是多少?
(应用)求从下到上前33个台阶上数的和.
(发现)试用含![]() (
(![]() 为正整数)的式子表示出数“-2”所在的台阶数(此问直接写出结果).
为正整数)的式子表示出数“-2”所在的台阶数(此问直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线![]() 与
与![]()
(1)在同一平面直角坐标系中作出两直线的图象;
(2)求出两直线的交点;
(3)根据图象指出x为何值时,![]() ;
;
(4)求这两条直线与x轴围成的三角形面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com