
【题目】如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.
(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD的长;若不能,请说明理由;
(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作ADEF.
①ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.
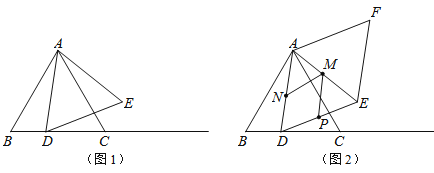
【答案】(1)不存在;(2)①存在,6![]() ;②3.
;②3.
【解析】试题分析:(1)根据等边三角形的性质可知: ![]() 由三角形外角的性质可知
由三角形外角的性质可知![]() 从而可知:
从而可知: ![]() 所以
所以![]() 点E不能移动到直线AB上.
点E不能移动到直线AB上.
(2)因为△ADE的面积![]() 所以当AD最短时,△ADE的面积有最小,根据垂线段最短可知当AD⊥BC时,△ADE的面积最小.四边形
所以当AD最短时,△ADE的面积有最小,根据垂线段最短可知当AD⊥BC时,△ADE的面积最小.四边形![]() 为平四边形,AE为对角线,所以平行四边形
为平四边形,AE为对角线,所以平行四边形![]() 的面积是△ADE面积的2倍,所以△ADE的面积最小时,平行四边形的面积最小;
的面积是△ADE面积的2倍,所以△ADE的面积最小时,平行四边形的面积最小;
(3)当点N、M、P在一条直线上,且NP⊥AD时,MN+MP有最小值,最小值为AD与EF之间的距离.
试题解析:(1)不存在.
理由:如图1所示:
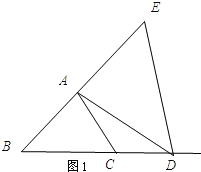
∵△ABC和△ADE均为等边三角形,
∴![]()
∵![]()
∴![]()
又∵![]()
∴![]()
∴点E不能移动到直线AB上.
(2)①存在:在图(2)中,当AD⊥BC时,△ADE的面积最小.

在Rt△ADB中, ![]()
∴△ADE的面积![]()
∵四边形ADEF为平四边形,AE为对角线,
∴平行四边形ADEF的面积是△ADE面积的2倍.
∴ADEF的面积的最小值![]()
②如图3所示:作点P关于AE的对称点P1,
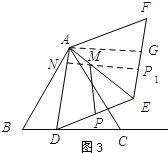
当点N、M、P在一条直线上,且NP⊥AD时,MN+MP有最小值,
过点A作AG∥NP1,
∵AN∥GP1,AG∥NP,
∴四边形ANP1G为平行四边形.
∴![]()
即MN+MP的最小值为3.


科目:初中数学 来源: 题型:
【题目】计算题
(1)6+(﹣![]() )﹣2﹣(﹣1.5).
)﹣2﹣(﹣1.5).
(2)﹣66×4﹣(﹣2.5)÷(﹣0.1).
(3)(![]() )×12.
)×12.
(4)![]() .
.
(5)(﹣2)2×5﹣(﹣2)3÷4.
(6)(﹣10)4+[(﹣4)2﹣(3+32)×2].
(7)![]() .
.
(8)(﹣2)2+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )
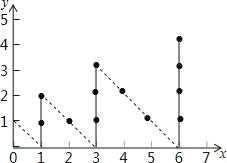
A. 886 B. 903 C. 946 D. 990
查看答案和解析>>
科目:初中数学 来源: 题型:
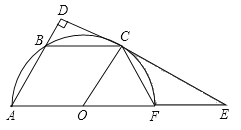
【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)若半圆O的半径为6,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点表示的数为
的中点表示的数为![]() .
.
(问题情境)
如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为![]() 秒(
秒(![]() ).
).
(综合运用)
(1)填空:
①![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ________,线段
________,线段![]() 的中点表示的数为__________.
的中点表示的数为__________.
②用含![]() 的代数式表示:
的代数式表示:![]() 秒后,点
秒后,点![]() 表示的数为____________;点
表示的数为____________;点![]() 表示的数为___________.
表示的数为___________.
③当![]() _________时,
_________时,![]() 、
、![]() 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.
(2)当![]() 为何值时,
为何值时,![]() .
.
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx﹣2与x轴交于点A(﹣1,0),B(4,0)两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).
(1)求该抛物线的解析式;
(2)如图2,过点A作BE的平行线交抛物线于另一点D,点P是抛物线上位于线段AD下方的一个动点,连结PA,EA,ED,PD,求四边形EAPD面积的最大值;
(3)如图3,连结AC,将△AOC绕点O逆时针方向旋转,记旋转中的三角形为△A′OC′,在旋转过程中,直线OC′与直线BE交于点Q,若△BOQ为等腰三角形,请直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
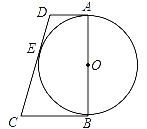
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=![]() 图象的一部分.其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,
图象的一部分.其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,![]() ),
),![]() 是抛物线上两点,则
是抛物线上两点,则![]() >
>![]() .其中说法正确的是_____ (填序号)
.其中说法正确的是_____ (填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com