
【题目】如图是二次函数y=![]() 图象的一部分.其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,
图象的一部分.其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,![]() ),
),![]() 是抛物线上两点,则
是抛物线上两点,则![]() >
>![]() .其中说法正确的是_____ (填序号)
.其中说法正确的是_____ (填序号)

【答案】(1)(2)(4)
【解析】分析:根据图象分别求出a、b、c的符号,即可判断(1),根据对称轴求出b=2a,代入2a-b即可判断(2),把x=2代入二次函数的解析式,再根据二次函数的性质即可判断(3),求出点(-5,y1)关于直线x=-1的对称点的坐标,根据对称轴判断y1和y2的大小,即可判断(4).
详解:∵二次函数的图象开口向上,
∴a>0,
∵二次函数的图象交y轴的负半轴于一点,
∴c<0,
∵对称轴是直线x=-1,
∴-![]() =-1,
=-1,
∴b=2a>0,
∴abc<0,
故(1)正确;
∵b=2a,
∴2a-b=0,
故(2)正确;
∵抛物线的对称轴为x=-1,且过点(-3,0),
∴抛物线与x轴另一交点为(1,0).
∵当x>-1时,y随x的增大而增大,
∴当x=2时y>0,即4a+2b+c>0,
故(3)错误;
∵(-5,y1)关于直线x=-1的对称点的坐标是(3,y1),
又∵当x>-1时,y随x的增大而增大,3>![]() ,
,
∴y1>y2,
故(4)正确;
故答案为(1)(2)(4).


科目:初中数学 来源: 题型:
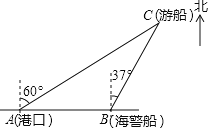
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,
(1)求点C到直线AB的距离;
(2)求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.
(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD的长;若不能,请说明理由;
(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作ADEF.
①ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.
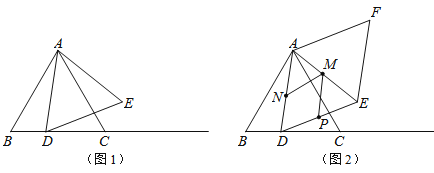
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元;超过10吨时,超过部分按每吨1.8元收费,该市某户居民5月份用水![]() 吨
吨![]() ,应缴水费
,应缴水费![]() 元.
元.
(1)写出![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)某户居民若5月份用水16吨,应缴水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.
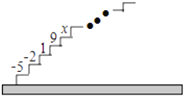
(尝试)(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数![]() 是多少?
是多少?
(应用)求从下到上前33个台阶上数的和.
(发现)试用含![]() (
(![]() 为正整数)的式子表示出数“-2”所在的台阶数(此问直接写出结果).
为正整数)的式子表示出数“-2”所在的台阶数(此问直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
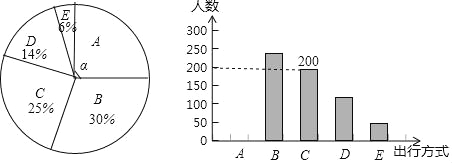
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠ABC=90°,AB=3,BC=4,点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图①)或线段AB的延长线(如图②)于点P.
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
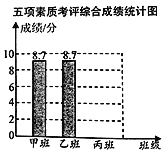
【题目】学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为县级先进班集体,下表是三个班的五项素质考评得分表。
五项素质考评得分表(单位:分)
班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
甲班 | 10 | 10 | 6 | 10 | 7 |
乙班 | 10 | 8 | 8 | 9 | 8 |
丙班 | 9 | 10 | 9 | 6 | 9 |
根据统计表中的信息回答下列问题:
(1)请你补全五项成绩考评分析表中的数据:
班级 | 平均分 | 众数 | 中位数 |
甲班 | 8.6 | 10 | ③ |
乙班 | 8.6 | ② | 8 |
丙班 | ① | 9 | 9 |
(2)参照上表中的数据,你推荐哪个班为县级先进班集体?并说明理由。
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照3∶2∶1∶1∶3的比确定班级的综合成绩,学生处的李老师根据这个综合成绩,绘制了一幅不完整的条形统计图,请将这个统计图补充完整,按照这个成绩,应推荐哪个班为县级先进班集体?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, l1∥l2,∠1 = 105°,∠2 = 140°,则∠α = _____________.
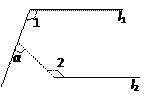
【答案】65°
【解析】分析:反向延长CD交AE于点F,根据平行线的性质得到![]() 根据三角形外角的性质得到
根据三角形外角的性质得到![]() 即可求出.
即可求出.
详解:如图:反向延长CD交AE于点F,
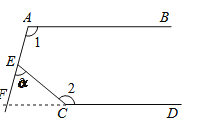
∵AB∥CD,![]()
∴![]()
∵![]()
∴![]()
故答案为:![]()
点睛:考查平行线的性质和三角形外角的性质,解题的关键是作出辅助线.
【题型】填空题
【结束】
14
【题目】如图,AD是⊙O的直径,AD=12,点B、C在⊙O上,AB、DC的延长线交于点E,且CB=CE,∠BCE=70°.
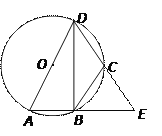
有以下结论:①∠ADE=∠E;②劣弧![]() 的长为
的长为![]() ;③点C为
;③点C为![]() 的中点;④BD平分∠ADE.以上结论一定正确的是_________________.(把正确结论的序号都填上)
的中点;④BD平分∠ADE.以上结论一定正确的是_________________.(把正确结论的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com