
【题目】学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为县级先进班集体,下表是三个班的五项素质考评得分表。
五项素质考评得分表(单位:分)
班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
甲班 | 10 | 10 | 6 | 10 | 7 |
乙班 | 10 | 8 | 8 | 9 | 8 |
丙班 | 9 | 10 | 9 | 6 | 9 |
根据统计表中的信息回答下列问题:
(1)请你补全五项成绩考评分析表中的数据:
班级 | 平均分 | 众数 | 中位数 |
甲班 | 8.6 | 10 | ③ |
乙班 | 8.6 | ② | 8 |
丙班 | ① | 9 | 9 |
(2)参照上表中的数据,你推荐哪个班为县级先进班集体?并说明理由。
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照3∶2∶1∶1∶3的比确定班级的综合成绩,学生处的李老师根据这个综合成绩,绘制了一幅不完整的条形统计图,请将这个统计图补充完整,按照这个成绩,应推荐哪个班为县级先进班集体?为什么?
【答案】(1)8.6,8,10;(2)甲班:三个班的平均数相同,甲班众数与中位数高于乙和丙;(3)画图见解析,丙班.
【解析】
(1)根据平均数是所有数据的和除以数据的个数,众数是出现次数最多的数据,中位数是一组数据按从小到大或从大到小的顺序排列中间的数(或中间两个数的平均数),可得答案;
(2)根据平均数、众数、中位数的大小比较,可得答案;
(3)根据加权平均数的大小比较,可得答案.
(1) ①![]() =(9+10+9+6+9)
=(9+10+9+6+9)![]() =8.6,②观察五项素质考评得分表可知乙班的众数是8,③观察五项素质考评得分表可知甲班的中位数是10;
=8.6,②观察五项素质考评得分表可知乙班的众数是8,③观察五项素质考评得分表可知甲班的中位数是10;
(2)甲班,理由为:三个班的平均数相同,甲班的众数与中位数都高于乙班与丙班;
(3)根据题意,得:丙班的平均数为9×![]() +10×
+10×![]() +9×
+9×![]() +6×
+6×![]() +9×
+9×![]() =8.9
=8.9
补全条形统计图,如图所示
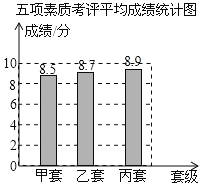
∵8.5<8.7<8.9,
∴依照这个成绩,应推荐丙班为市级先进班集体.


科目:初中数学 来源: 题型:
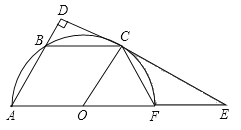
【题目】如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)若半圆O的半径为6,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=![]() 图象的一部分.其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,
图象的一部分.其对称轴为x=-1,且过点(-3,0).下列说法:(1)abc<0;(2)2a-b=0;(3)4a+2b+c=0;(4)若(-5,![]() ),
),![]() 是抛物线上两点,则
是抛物线上两点,则![]() >
>![]() .其中说法正确的是_____ (填序号)
.其中说法正确的是_____ (填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用的练习本可以到甲商店购买,也可以到乙商店购买,已知两商店的标价都是每本1元,甲商店的优惠条件是:购买10本以上,从第11本开始按标价的70%卖;乙商店的优惠条件是:每本按标价的80%卖.
(1)小明要买20本时,到哪个商店较省钱?
(2)买多少本时到两个商店付的钱一样?
(3)小明现有32元钱,最多可买多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,且BC=2AF。
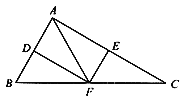
(1)求证:四边形ADEF为矩形;
(2)若∠C=30°、AF=2,写出矩形ADEF的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,AD=![]() ,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
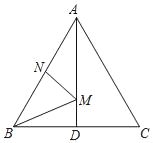
A. ![]() B. 2C. 1D. 3
B. 2C. 1D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪对本班全体同学的兴趣爱好进行了一次调查,根据采集到的数据绘制了如图的统计图,请你根据图中提供的信息解答下列问题:
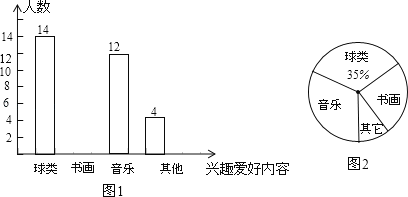
(1)该班学生共多少人;
(2)在图1中,请你将统计图补充完整;
(3)求爱好“书画”的学生数占该班学生数的百分比;
(4)在图2中,“音乐”部分所对应的圆心角度数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com