
【题目】计算题
(1)6+(﹣![]() )﹣2﹣(﹣1.5).
)﹣2﹣(﹣1.5).
(2)﹣66×4﹣(﹣2.5)÷(﹣0.1).
(3)(![]() )×12.
)×12.
(4)![]() .
.
(5)(﹣2)2×5﹣(﹣2)3÷4.
(6)(﹣10)4+[(﹣4)2﹣(3+32)×2].
(7)![]() .
.
(8)(﹣2)2+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2).
【答案】(1)5.3;(2)-289;(3)-1;(4)-![]() ;(5)22;(6)9992;(7)﹣4
;(5)22;(6)9992;(7)﹣4![]() ;(8)﹣45.5.
;(8)﹣45.5.
【解析】
(1)原式利用减法法则变形,计算即可求出值;
(2)原式先计算乘除运算,再计算加减运算即可求出值;
(3)原式利用乘法分配计算即可求出值;
(4)原式利用乘法法则计算即可求出值;
(5)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可求出值;
(6)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可求出值;
(7)原式先计算绝对值运算,再计算乘法运算,最后算加减运算即可求出值;
(8)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可求出值.
解:(1)原式=6﹣0.2﹣2+1.5=5.3;
(2)原式=﹣264﹣25=﹣289;
(3)原式=3+2﹣6=﹣1;
(4)原式=![]() ﹣
﹣![]() =-
=-![]() ;
;
(5)原式=20+2=22;
(6)原式=10000+16﹣24=9992;
(7)原式=﹣![]() ﹣
﹣![]() ﹣
﹣![]() ﹣3=﹣4
﹣3=﹣4![]() ;
;
(8)原式=4﹣3×18+![]() =﹣45.5.
=﹣45.5.


科目:初中数学 来源: 题型:
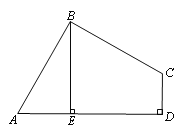
【题目】已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.
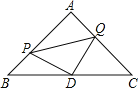
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线l和l外一点P.(如图1)
求作:直线l的垂线,使它经过点P.
作法:如图2
(1)在直线l上任取两点A,B;
(2)分别以点A,B为圆心,AP,BP长为半径作弧,两弧相交于点Q;
(3)作直线PQ.
所以直线PQ就是所求的垂线.
请回答:该作图的依据是_________________________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知树枝AB长为1.将树枝AB按照如下规则进行分形.其中1级分形图中,由B点处生长出两条树枝BD,BE,每条树枝长均为AB长的一半;在2级分形图中,D、E两点处生长出的每条树枝都等于DB长的一半.按照上面分形方法得到3级、4级分形图形.
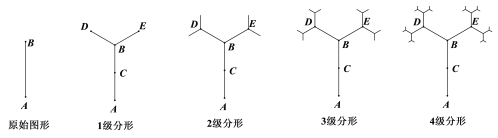
按照上面的规律,在3级分形图中,树枝长度的总和是_____________;
在n级分形图中,树枝总条数是___________(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() (m>0)与x轴的交点为A,B.
(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为16, G、H分别为AB. AC的中点,分别以AB.AC为斜边向外作Rt△ADB和Rt△AEC,连接DG.GH,EH,则DG+GH+EH的值为__________.
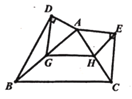
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,
(1)求点C到直线AB的距离;
(2)求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
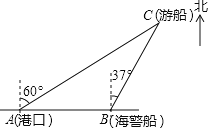
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.
(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD的长;若不能,请说明理由;
(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作ADEF.
①ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.
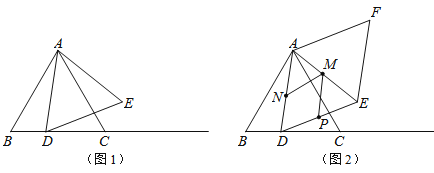
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com