
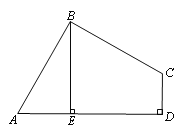
【题目】已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
【答案】(1)(2)证明见解析
【解析】
(1)题目中存在直角,垂直,含线段平方的等式,因此考虑连接AC,构造直角三角形,利用勾股定理证明
(2)可采用“截长”法证明,过点C作CF⊥BE于F,易证CD=EF,只需再证明AE=BF即可,这一点又可通过全等三角形获证.
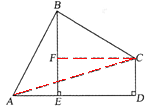
解:(1)证明:连接AC。
∵∠ABC=90°,∴AB2+BC2=AC2。
∵CD⊥AD,∴AD2+CD2=AC2。
∵AD2+CD2=2AB2,
∴AB2+BC2=2AB2
∴AB=BC。
(2)证明:过C作CF⊥BE于F
∵BE⊥AD,∴四边形CDEF是矩形
∴CD=EF
∵∠ABE+∠BAE=90°,∠ABE+∠CBF=90
∴∠BAE=∠CBF。
又∵AB=BC,∠BEA=∠CFB,
∴△BAE≌△CBF(AAS)
∴AE=BF。
∴BE=BF+EF =AE+CD


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】你会玩“24点”游戏吗?从一副扑克牌(去掉大、小王)中任意抽取四张,根据牌面上的数字进行混合运算(每一张牌必须用一次且只能用一次,可以加括号),使得运算结果为24或﹣24,其中红色扑克牌代表负数,黑色扑克牌代表正数.J.Q.K.A分别代表11.12.13.1,小明抽到了黑桃7,黑桃3,梅花3,梅花7,他运用下面的方法凑成了:![]() .
.
(1)如果抽到的是黑桃7,黑桃5,红桃5,梅花7,你能凑成24吗?
(2)如果抽到的是黑桃A,方块2,黑桃2,黑桃3,你能凑成24吗?(请用两种方法)
(3)如果抽到的是黑桃Q,红桃Q,梅花3,方块A,你能凑成24吗?(请用多种方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保证达万高速公路在2012年底全线顺利通车,某路段规定在若干天内完成修建任务.已知甲队单独完成这项工程比规定时间多用10天,乙队单独完成这项工程比规定时间多用40天,如果甲、乙两队合作,可比规定时间提前14天完成任务.若设规定的时间为x天,由题意列出的方程是( )
A.![]() +
+![]() =
=![]() B.
B.![]() +
+![]() =
=![]()
C.![]() -
-![]() =
=![]() D.
D.![]() +
+![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在直角梯形ABCD中, AD∥BC,∠BCD=90°, BC=CD=2AD , E、F分别是BC、CD边的中点,连结BF、DE交于点P,连结CP并延长交AB于点Q,连结AF,则下列结论不正确的是( )
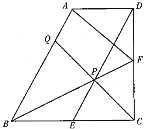
A.CP 平分∠BCDB.四边形 ABED 为平行四边形
C.CQ将直角梯形 ABCD 分为面积相等的两部分D.△ABF为等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:
①S1+S2=S3+S4② S2+S4= S1+ S3
③若S3=2S1,则S4=2S2④若S1= S2,则P点在矩形的对角线上
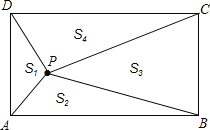
其中正确的结论的序号是 ▲ (把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是数轴上表示-2与-1两数的点为端点的线段的中点.
![]()
(1)数轴上点P表示的数为 ;
(2)在数轴上距离点P为2.5个单位长度的点表示的数为 ;
(3)如图,若点P是线段AB(点A在点B的左侧)的中点,且点A表示的数为m,那么点B表示的数是 .(用含m的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
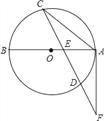
【题目】如图,已知AB是⊙O的直径,弦CD与AB交于点E,F为CD的延长线上一点,连接AF,且FA2=FDFC.
(1)求证:FA为⊙O的切线;
(2)若AC=8,CE:ED=6:5,AE:EB=2:3,求AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.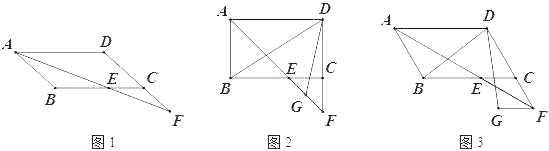
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)6+(﹣![]() )﹣2﹣(﹣1.5).
)﹣2﹣(﹣1.5).
(2)﹣66×4﹣(﹣2.5)÷(﹣0.1).
(3)(![]() )×12.
)×12.
(4)![]() .
.
(5)(﹣2)2×5﹣(﹣2)3÷4.
(6)(﹣10)4+[(﹣4)2﹣(3+32)×2].
(7)![]() .
.
(8)(﹣2)2+(﹣3)×[(﹣4)2+2]﹣(﹣3)2÷(﹣2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com