
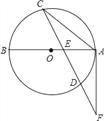
【题目】如图,已知AB是⊙O的直径,弦CD与AB交于点E,F为CD的延长线上一点,连接AF,且FA2=FDFC.
(1)求证:FA为⊙O的切线;
(2)若AC=8,CE:ED=6:5,AE:EB=2:3,求AB的值.
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】中小学生每天在校体育活动时间不低于1小时”![]() 为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生
为此,我区就“你每天在校体育活动时间是多少”的问题随机调查了区内300名初中学生![]() 根据调查结果绘制成的统计图
根据调查结果绘制成的统计图![]() 部分
部分![]() 如图所示,其中分组情况是:
如图所示,其中分组情况是:
A组:![]() B组:
B组:![]() C组:
C组:![]() D组:
D组:![]()
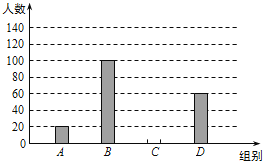
请根据上述信息解答下列问题:
![]() 组的人数是______.
组的人数是______.
![]() 本次调查数据的中位数落在______组内;
本次调查数据的中位数落在______组内;
![]() 若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
若我区有5400名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
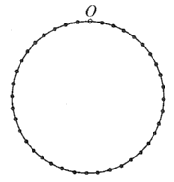
【题目】在学校科技周活动中,丛明和蔡智同学制作的智能小车![]() ,
,![]() 做圆周(等分为
做圆周(等分为![]() 格)运动,规定顺时针方向为负运动,逆时针方向为正运动.若两小车
格)运动,规定顺时针方向为负运动,逆时针方向为正运动.若两小车![]() ,
,![]() 从
从![]() 点同时出发,当它们按
点同时出发,当它们按![]() 的速度运动到
的速度运动到![]() 秒时,共行
秒时,共行![]() 格.
格.
(1)求两小车的运动速度;若![]() 作正运动,
作正运动,![]() 作负运动,标出小车运动到
作负运动,标出小车运动到![]() 秒时的位置
秒时的位置![]() ,
,![]() ;
;
(2)若![]() ,
,![]() 从(1)中的位置同时出发,都沿正方向运动,再经多久时
从(1)中的位置同时出发,都沿正方向运动,再经多久时![]() ,
,![]() 所到达位置表示的数互为相反数?
所到达位置表示的数互为相反数?
(3)若![]() ,
,![]() 从(2)中的位置同时出发相向运动,当它们在
从(2)中的位置同时出发相向运动,当它们在![]() 点相遇时,
点相遇时,![]() 点所对应的数是多少?
点所对应的数是多少?
(4)若![]() ,
,![]() 从(3)中的位置同时出发,都沿负方向运动,经过多长时间
从(3)中的位置同时出发,都沿负方向运动,经过多长时间![]() ,
,![]() 首次相遇?
首次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
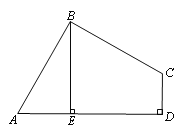
【题目】已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两支“徒步队”到野外沿相同路线徒步,徒步的路程为24千米.甲队步行速度为4千米/时,乙队步行速度为6千米/时.甲队出发1小时后,乙队才出发,同时乙队派一名联络员跑步在两队之间来回进行一次联络(不停顿),他跑步的速度为10千米/时.
(1)乙队追上甲队需要多长时间?
(2)联络员从出发到与甲队联系上后返回乙队时,他跑步的总路程是多少?
(3)从甲队出发开始到乙队完成徒步路程时止,何时两队间间隔的路程为1千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
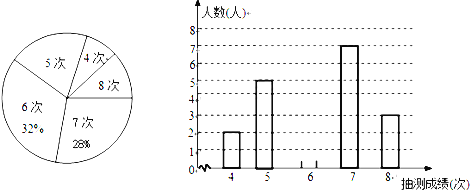
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请将条形图补充完整;
(3)若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,菱形ABCD中,对角线![]() 相交于点O,且
相交于点O,且![]() 点P从点B出发,沿BA方向匀速运动,速度为
点P从点B出发,沿BA方向匀速运动,速度为![]() ;同时,直线EF从点D出发,沿DB方向匀速运动,速度为
;同时,直线EF从点D出发,沿DB方向匀速运动,速度为![]() ,且与
,且与![]() 分别交于点
分别交于点![]() ;当直线EF停止运动时,点P也停止运动
;当直线EF停止运动时,点P也停止运动![]() 连接PF,设运动时间为
连接PF,设运动时间为![]() 设四边形APFE的面积为
设四边形APFE的面积为![]() ,则下列图象中,能表示y与t的函数关系的图象大致是
,则下列图象中,能表示y与t的函数关系的图象大致是![]()

A. 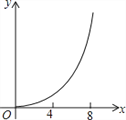 B.
B. 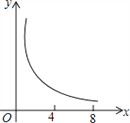 C.
C. 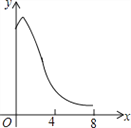 D.
D. 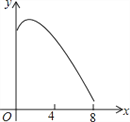
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.
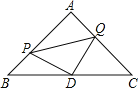
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为16, G、H分别为AB. AC的中点,分别以AB.AC为斜边向外作Rt△ADB和Rt△AEC,连接DG.GH,EH,则DG+GH+EH的值为__________.
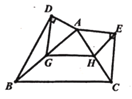
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com