
【题目】甲、乙两支“徒步队”到野外沿相同路线徒步,徒步的路程为24千米.甲队步行速度为4千米/时,乙队步行速度为6千米/时.甲队出发1小时后,乙队才出发,同时乙队派一名联络员跑步在两队之间来回进行一次联络(不停顿),他跑步的速度为10千米/时.
(1)乙队追上甲队需要多长时间?
(2)联络员从出发到与甲队联系上后返回乙队时,他跑步的总路程是多少?
(3)从甲队出发开始到乙队完成徒步路程时止,何时两队间间隔的路程为1千米?
【答案】(1) 2小时;(2)8.75千米;(3)2.5小时或3.5小时或5.75小时两队间间隔的路程为1千米
【解析】分析:(1)设乙队追上甲队需要x小时,根据乙队比甲队快的速度×时间=甲队比乙队先走的路程可列出方程,解出即可得出时间;
(2)先计算出联络员所走的时间,再由路程=速度×时间即可得出联络员走的路程.
(3)要分3种情况讨论:①当甲队出发1小时后,相遇前与乙队相距1千米;②当甲队出发1小时后,相遇后与乙队相距1千米;③乙队到达后两队间间隔的路程为1千米;分别列出方程求解即可.
详解:(1)设乙队追上甲队需要x小时,
根据题意得:![]()
解得:![]()
答:乙队追上甲队需要2小时.
(2)4×1÷(6+10)=0.25(小时),
[(1+0.25)×4﹣0.25×10]÷(10﹣6)
=2.5÷4
=0.625(小时),
(0.25+0.625)×10=8.75(千米).
答:他跑步的总路程是8.75千米.
(3)要分三种情况讨论:
设t小时两队间间隔的路程为1千米,则
①当甲队出发1小时后,相遇前与乙队相距1千米,
由题意得![]()
解得:![]()
②当甲队出发1小时后,相遇后与乙队相距1千米,
由题意得:![]()
解得:![]()
③乙队到达后两队间间隔的路程为1千米,
由题意得:![]()
解得:![]()
答:2.5小时或3.5小时或5.75小时两队间间隔的路程为1千米.


科目:初中数学 来源: 题型:
【题目】已知点A,B是数轴上的点,且点A表示数-3,请参照图并思考,完成下列各题:
![]()
(1)将A点向右移动4个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是 .
(2)若把数轴绕点A对折,则对折后,点B落在数轴上的位置所表示的数为 .
(3)若(1)中点B以每秒2个单位长度沿数轴向左运动,A不动,多长时间后,点B与点A距离为2个单位长度?试列式计算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在AB上,点M、N分别是AC、BC的中点,
(1)若AC=12cm,BC=10cm,求线段MN的长;
(2)若点C为线段AB上任意一点,满足AC+BC=acm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若点C在线段AB的延长线上,且满足AC-BC=bcm,点M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.请用一句简洁的话描述你发现的结论.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B都在数轴上,O为原点.
(1)点B表示的数是_________________;
(2)若点B以每秒2个单位长度的速度沿数轴向右运动,则2秒后点B表示的数是________;
(3)若点A、B分别以每秒1个单位长度、3个单位长度的速度沿数轴向右运动,而点O不动,t秒后,A、B、O三个点中有一个点是另外两个点为端点的线段的中点,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展![]() 某旅游公司对我市一企业个人旅游年消费情况进行问卷调查
某旅游公司对我市一企业个人旅游年消费情况进行问卷调查![]() 随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
组别 | 个人年消费金额 | 频数 | 频率 |
A |
| 18 |
|
B |
| a | b |
C |
|
|
|
D |
| 24 |
|
E |
| 12 |
|
合计 | c |
| |

根据以上信息解答下列问题:
![]() ________;
________; ![]() ________;
________; ![]() ________;
________;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.
若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 ![]() 的值为( )
的值为( ) 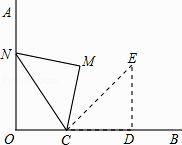
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2 , 若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x=1.
其中正确的有( )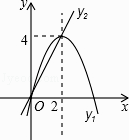
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= ![]() (m≠0)交于点A(2,﹣3)和点B(n,2).
(m≠0)交于点A(2,﹣3)和点B(n,2). 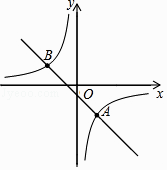
(1)求直线与双曲线的表达式;
(2)对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= ![]() (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
(m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( ) 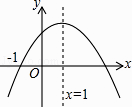
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com