练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

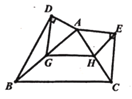
    【题目】如图，△ABC的周长为16, G、H分别为AB. AC的中点，分别以AB.AC为斜边向外作Rt△ADB和Rt△AEC,连接DG.GH,EH,则DG+GH+EH的值为__________.

    【答案】8

    【解析】

    根据直角三角形斜边上的中线等于斜边的一半可得DG=0.5AB，EH=0.5AC，三角形的中位线平行于第三边并且等于第三边的一半可得GH=0.5BC，然后求出DG+GH+EH的值为△ABC的一半．

    解：∵G、H分别为AB、AC的中点，△ADB和△AEC为直角三角形，

    ∴DG=0.5AB，EH=0.5AC，

    ∴GH为△ABC的中位线，

    ∴GH=0.5BC，

    ∴DG+GH+EH=0.5（AB+AC+BC）=0.5×16=8，故答案为：8.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

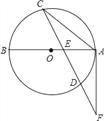
    【题目】如图，已知AB是⊙O的直径，弦CD与AB交于点E，F为CD的延长线上一点，连接AF，且FA2=FDFC．

    （1）求证：FA为⊙O的切线；

    （2）若AC=8，CE：ED=6：5，AE：EB=2：3，求AB的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】南昌的雾霾引起了小张对环保问题的重视．一次旅游小张思考了一个问题．从某地到南昌，若乘火车需要小时，若乘汽车需要小时．这两种交通工具平均每小时二氧化碳的排放量之和为千克，火车全程二氧化碳的排放总量比汽车的多千克，分别求火车和汽车平均每小时二氧化碳的排放量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算题

    （1）6+（﹣）﹣2﹣（﹣1.5）．

    （2）﹣66×4﹣（﹣2.5）÷（﹣0.1）．

    （3）（）×12．

    （4）．

    （5）（﹣2）2×5﹣（﹣2）3÷4．

    （6）（﹣10）4+[（﹣4）2﹣（3+32）×2]．

    （7）．

    （8）（﹣2）2+（﹣3）×[（﹣4）2+2]﹣（﹣3）2÷（﹣2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等边△ABC中：

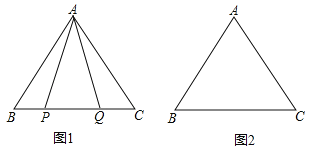
    （1）如图1，P，Q是BC边上的两点，AP=AQ，∠BAP=20°，求∠AQB的度数；

    （2）点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC的对称点为M，连接AM，PM．

    ①依题意将图2补全；

    ②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

    想法1：要证明PA=PM，只需证△APM是等边三角形；

    想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；

    想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…

    请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

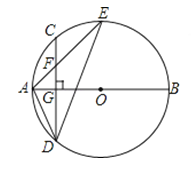
    【题目】如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足，连接AF并延长交⊙O于点E，连接AD、DE，若CF＝2，AF＝3．给出下列结论：①△ADF∽△AED；②FG＝2；③tan∠E＝；

    ④S△DEF＝．其中正确的是结论的个数是（ ）

    (A)1 (B)2 (C)3 (D)4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

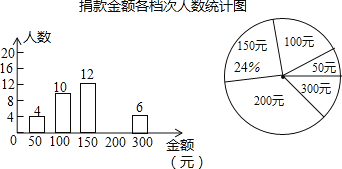
    【题目】企业举行“爱心一日捐”活动，捐款金额分为五个档次，分别是50元，100元，150元，200元，300元．宣传小组随机抽取部分捐款职工并统计了他们的捐款金额，绘制成两个不完整的统计图，请结合图表中的信息解答下列问题：

    （1）宣传小组抽取的捐款人数为_____人，请补全条形统计图；

    （2）在扇形统计图中，求100元所对应扇形的圆心角的度数；

    （3）已知该企业共有500人参与本次捐款，请你估计捐款总额大约为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一个粒子从原点出发，每分钟移动一次，依次运动到（0，1）→（1，0）→（1，1）→（1，2）→（2，1）→…，则2015分钟时粒子所在点的横坐标为（　　）

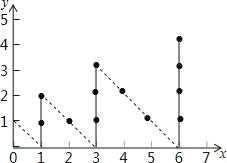
    A. 886 B. 903 C. 946 D. 990

    查看答案和解析>>

    科目：初中数学 来源： 题型：

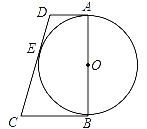
    【题目】如图所示，AB是⊙O的直径，AD与⊙O相切于点A，DE与⊙O相切于点E，点C为DE延长线上一点，且CE=CB．

    （1）求证：BC为⊙O的切线；

    （2）若AB=4，AD=1，求线段CE的长．

    查看答案和解析>>

    同步练习册答案