
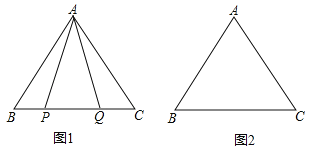
【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).
【答案】(1)40°;(2)①作图见解析;②证明见解析.
【解析】
试题分析:(1)根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,根据三角形外角的性质即可得到结论;
(2)①根据要求作出图形,如图2;
②根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,由点Q关于直线AC的对称点为M,得到AQ=AM,∠OAC=∠MAC,等量代换得到∠MAC=∠BAP,推出△APM是等边三角形,根据等边三角形的性质即可得到结论.
试题解析:(1)∵AP=AQ,∴∠APQ=∠AQP,∴∠APB=∠AQC,∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠BAP=∠CAQ=20°,∴∠PAQ=∠BAC﹣∠BAP﹣∠CAQ=60°﹣20°﹣20°=20°,∴∠BAQ=∠BAP+∠PAQ=40°;
(2)①如图2;
②∵AP=AQ,∴∠APQ=∠AQP,∴∠APB=∠AQC,∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠BAP=∠CAQ,∵点Q关于直线AC的对称点为M,∴AQ=AM,∠QAC=∠MAC,∴∠MAC=∠BAP,∴∠BAP+∠PAC=∠MAC+∠CAP=60°,∴∠PAM=60°,∵AP=AQ,∴AP=AM,∴△APM是等边三角形,∴AP=PM.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】2017年9月12日,Apple(苹果公司)发布了iPhone X。苹果公司某生产车间计划平均每天生产iPhone X手机200台,但是由于种种原因,实际每天生产量与计划生产量相比有出入.下表是某周的生产情况(超产记为正,减产即为负)

(1)根据记录的数据可知该车间星期三生产iPhone X手机 台?
(2)产量最多的一天比产量最少的一天多生产iPhone X手机 台?
(3)根据记录的数据可知该车间本周实际共生产iPhone X手机多少台?(请写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于实数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[﹣π]=﹣4.如果[a]=﹣3,则a的取值范围为( )
A.﹣4<a≤﹣3
B.﹣4≤a<﹣3
C.﹣3<a≤﹣2
D.﹣3≤a<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
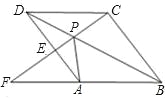
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线点F.问:
(1)图中△APD与哪个三角形全等?并说明理由;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两人同一地点出发后,路程随时间变化的图象.

(1)两个变量中, 是自变量, 是因变量;
(2)甲的速度 乙的速度(填<、=、或>);
(3)路程为150km时,甲行驶了 小时,乙行驶了 小时.
(4)甲比乙先走了 小时;在9时, 走在前面。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com