【题目】27的立方根是（ ）
A.9
B.﹣9
C.3
D.﹣3
科目：初中数学 来源： 题型：
【题目】一个材质均匀的正方体的每个面上标有数字1，2，3中的其中一个，其展开图如图所示，随机抛掷此正方体一次，则朝上与朝下的两面上数字相同的概率是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
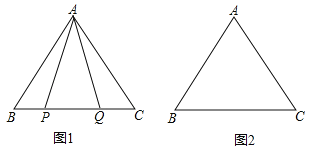
【题目】在等边△ABC中：
（1）如图1，P，Q是BC边上的两点，AP=AQ，∠BAP=20°，求∠AQB的度数；
（2）点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC的对称点为M，连接AM，PM．
①依题意将图2补全；
②小茹通过观察、实验提出猜想：在点P，Q运动的过程中，始终有PA=PM，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：要证明PA=PM，只需证△APM是等边三角形；
想法2：在BA上取一点N，使得BN=BP，要证明PA=PM，只需证△ANP≌△PCM；
想法3：将线段BP绕点B顺时针旋转60°，得到线段BK，要证PA=PM，只需证PA=CK，PM=CK…
请你参考上面的想法，帮助小茹证明PA=PM（一种方法即可）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某农户去年承包荒山若干亩，投资7800 元改造后，种果树2000棵．今年水果总产量为18000千克，此水果在市场上每千克售a元，在果园每千克售b元（b＜a）．该农户将水果拉到市场出售平均每天出售1000千克，需8 人帮忙，每人每天付工资25元，农用车运费及其他各项税费平均每天100元．
（1）分别用a，b表示两种方式出售水果的收入？
（2）若a=1.3元，b=1.1元，且两种出售水果方式都在相同的时间内售完全部水果，请你通过计算说明选择哪种出售方式较好．
（3）该农户加强果园管理，力争到明年纯收入达到15000元，那么纯收入增长率是多少？（纯收入=总收入﹣总支出，该农户采用了（2）中较好的出售方式出售）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一元二次方程4x2+5x=81化为一般形式后，二次项系数、一次项系数、常数项分别为（ ）
A.4，5，81
B.4，5，﹣81
C.4，5，0
D.4x2 ， 5x，﹣81
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现实生活中，如果收入1000元记作+1000元，那么﹣800表示（ ）
A. 支出800元 B. 收入800元 C. 支出200元 D. 收入200元
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场要经营一种新上市的文具，进价为20元/件。试营销阶段发现:当销售单价25元/件时，每天的销售量是250件；销售单价每上涨1元，每天的销售量就减少10件。
(1)写出商场销售这种文具，每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式。
(2)求销售单价为多少元时，该文具每天的销售利润最大?
(3)商场的营销部结合上述情况，提出了A,B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元；
方案B:每天销售量不少于10件，且每件文具的利润至少为25元。
请比较哪种方案的最大利润更高，并说明理由。（本题12分）
查看答案和解析>>
科目：初中数学 来源： 题型：
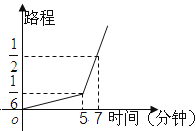
【题目】一名考生步行前往考场，5分钟走了总路程的
，估计步行不能准时到达，于是他改乘出租车赶往考场，他的行程与时间关系如图所示（假定总路程为1，出租车匀速），则他到达考场所花的时间比一直步行提前了________分钟。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
