
【题目】某农户去年承包荒山若干亩,投资7800 元改造后,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1000千克,需8 人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=1.3元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
(3)该农户加强果园管理,力争到明年纯收入达到15000元,那么纯收入增长率是多少?(纯收入=总收入﹣总支出,该农户采用了(2)中较好的出售方式出售)
【答案】(1)(18000a﹣5400)元,18000b元;(2)应选择在果园直接出售;(3)25%.
【解析】试题分析:(1)市场出售收入=水果的总收入-额外支出,而水果直接在果园的出售收入为:18000b.
(2)根据(1)中得到的代数式,将a=1.3,b=1.1,代入代数式计算即可.
(3)根据(2)的数据,首先确定今年的最高收入,然后计算增长率即可.
试题解析:(1)将这批水果拉到市场上出售收入为
18000a﹣![]() ×8×25﹣
×8×25﹣![]() ×100=18000a﹣3600﹣1800=18000a﹣5400(元)
×100=18000a﹣3600﹣1800=18000a﹣5400(元)
在果园直接出售收入为18000b元;
(2)当a=1.3时,市场收入为18000a﹣5400=18000×1.3﹣5400=18000(元).
当b=1.1时,果园收入为18000b=18000×1.1=19800(元)
因18000<19800,所以应选择在果园直接出售;
(3)因为今年的纯收入为19800﹣7800=12000, ![]() ×100%=25%,
×100%=25%,
所以增长率为25%.


科目:初中数学 来源: 题型:
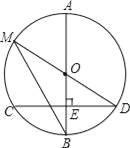
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
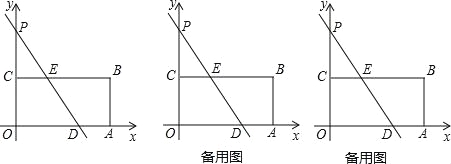
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=﹣![]() x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣![]() x+b平分矩形OABC的面积,求b的值;
x+b平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,当直线y=﹣![]() x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
(3)在(1)的条件下,将矩形OABC沿DE折叠,若点O落在边BC上,求出该点坐标;若不在边BC上,求将(1)中的直线沿y轴怎样平移,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
查看答案和解析>>
科目:初中数学 来源: 题型:
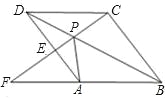
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线点F.问:
(1)图中△APD与哪个三角形全等?并说明理由;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
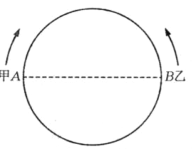
【题目】某校为培养青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏型.如图所示,甲、乙两点分别从直径的两端点 A、B以顺时针、逆时针的方向同时沿圆周运动. 甲运动的路程l(cm)与时间t(s)满足关系:![]() (t≥0),乙以4 cm/s的速度匀速运动,半圆的长度为 21 cm.
(t≥0),乙以4 cm/s的速度匀速运动,半圆的长度为 21 cm.
(1)甲运动 4 s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com